Load Balance Games

• Makespan scheduling on uniformly related machines

• n tasks with weights w1,…,wn

• m parallel mach in es with speeds s1,…,sm

  • identical machines: s1 = s2 = ··· = sm = 1 I uniformly related machines: else
  • A:[n]7→[m]…assignmentoftaskstomachines

• The load of machine j∈[m] under the assignment A is:

  

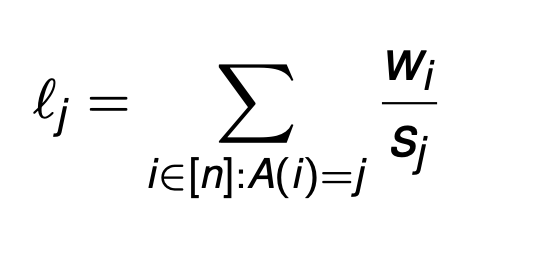
• Objective: minimize the make span, aka the maximum load overall machines

Definition of Load balancing games

• The task i∈[n] is managed by player i
• The pure strategy A(i) for each player i∈[n] yields an assignment A : [n] 7→ [m]
• Given an assignment A
  • the cost of player i is the load of the chosen machine l_A(i)
  • the social cost is the makespan: cost(A) = maxj∈[m]{l_j}

Pure Nash equilibrium

An assignment A is a pure Nash equilibrium if for all players i ∈ [n] and all machines j ∈ [m]:

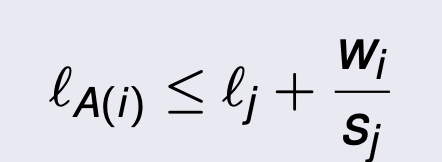
largest Processing Time (LPT)

• The Largest Processing Time (LPT) scheduling algorithm computes a pure Nash equilibrium in polynomial time. // 计算纯纳什均衡多项式时间

Algorithm

• Start with empty assignment: lj := 0 for all j ∈ [m]

• Sort task in non-increasing order w1 ≥ w2 ≥ ··· ≥ wn

• For i from 1 to n do

  • A(i) := arg minj∈[m]{lj + wi }
  • lA(i):=lA(i)+wi

• returnA

function LPTAlgorithm(arr) {
  var res = [];
  arr.forEach((val) => {});
}

Corollary 2.2

Every instance of the load balancing game admits a pure Nash equilibrium. // 所有负载平衡游戏的实例都可以使用纯纳什均衡

Best response sequences 1

• Improvement step: change to best response

  • Single player moves his task to the machine that minimizes his cost. // 减少花销

  • Example:

    

Best response sequences 2

• Best response sequences

  • take the strategic nature of the players into account

  • model convergence

• Theorem 2.3

  For every instance of the load balancing game with related machines every best response sequence terminates.

• Remark

  • There are instances with identical machine that have sequences of length Ω(2^√n).

Best response sequences 3

• Theorem 2.4

  • For identical machines the length of any sequence of best responses is at most 2^n. // 对于相同的机器，任何最佳响应序列的长度都不超过 2^n

• Theorem 2.5

  • Let A : [n] → [m] denote any assignment of n tasks to m identical machines. Starting from A, the max-weight best response policy reaches a pure Nash equilibrium after each agent was activated at most once.

• Lemma 2.6

  • Suppose task i makes a best response: For all tasks j with wj ≥ wi , if j was satisfied before, it remains satisfied after i’s best response.

Price of Anarchy: Definition

• Price of anarchy: The worst case ratio between the social cost in some Nash equilibrium (NE) and the optimum social cost.

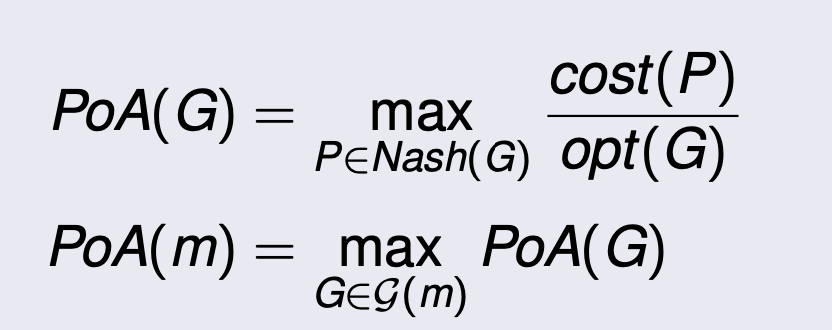
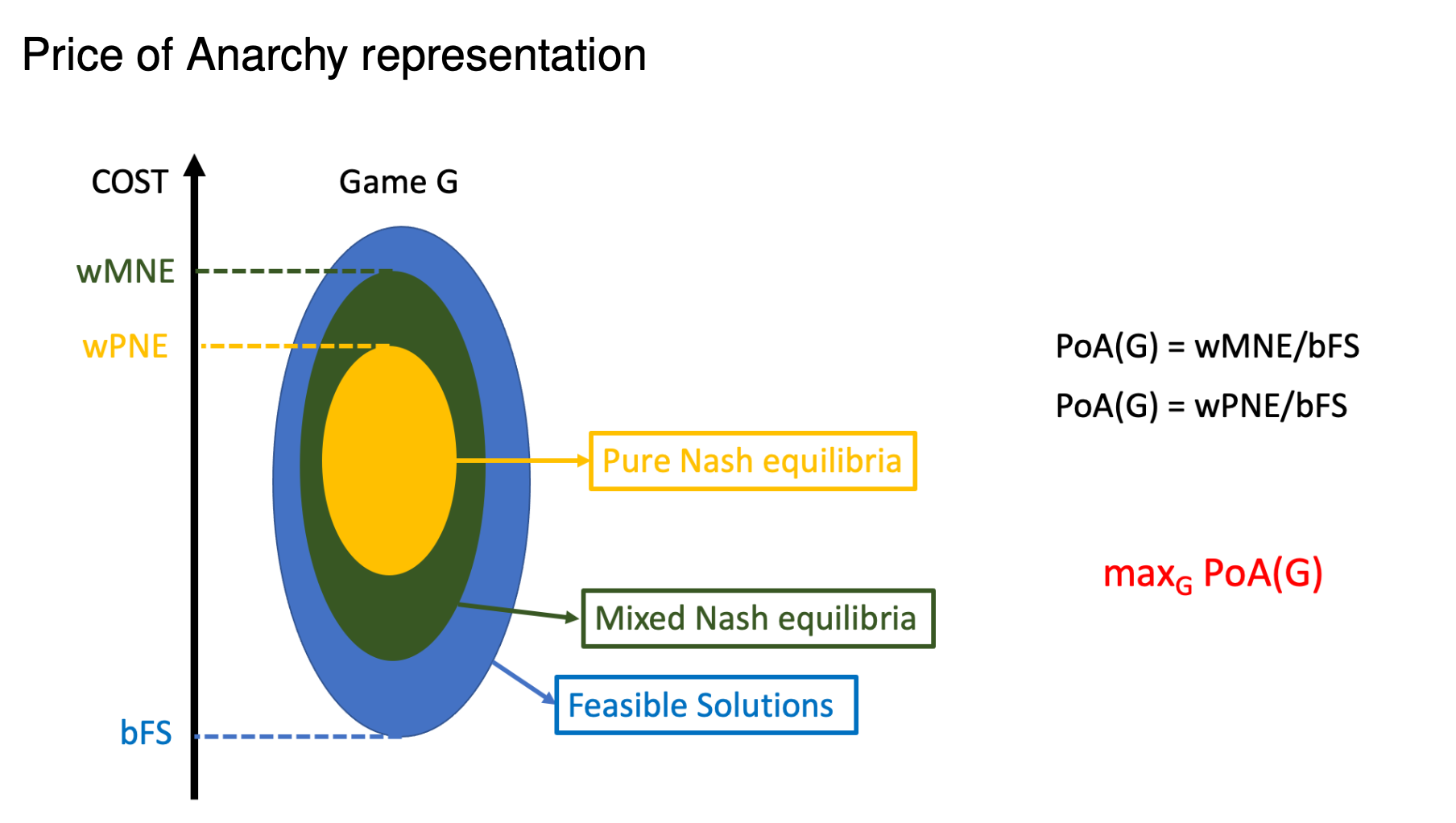
• Goal: Find the exact PoA for a class of games and type of equilibria.

• Upper bound α: show that for all such instances and all such equilibria the PoA is at most α.

• Lower bound α: find such an instance and such an equilibrium where the PoA is at least α.

Bounds on the Price of Anarchy

• Form=2,theexampleonpreviousslideprovesthelowerbound in blue.

• Exercise:

  Generalise this example to match the bound for all m.