Weighted Interval Scheduling 加权区间调度

Definition of Dynamic programming

• A technique for solving optimisation problems.

• The paradigm of dynamic programming:

• Given a problem P, define a sequence of subproblems, with the following properties: (定义一系列的子问题)

  • The subproblems are ordered from the smallest to the largest. 从小问题到大问题

  • The largest problem is our original problem P. 最大的问题是 P

  • The optimal solution of a subproblem can be constructed from the optimal solutions of sub-sub-problems. (Optimal Substructure). 子问题的最优解可以被更小的子子问题最优解解决

• Solve the subproblems from the smallest to the largest. When you solve a subproblem, store the solution (e.g., in an array) and use it to solve the larger subproblems.

Definition of Weighted Interval Scheduling

• A set of requests {1, 2, … , n}.

  • Request i has a starting time s(i), a finishing time f(i), and a value v(i).

  • Alternative view: Every request is an interval [s(i), f(i)] associated with a value v(i).

• Two requests i and j are compatible if their respective intervals do not overlap.

• Goal: Output a schedule which maximises the total value of compatible intervals.

Subset Sum

The subset sum problem

• We are given a set of n items {1, 2, … , n}.

• Each item i has a non-negative weight wi.

• We are given a bound W.

• Goal: Select a subset S of the items such that sum_i wi <= W and sum_i 𝑤i is maximised.

  

Dynamic Programming

• We need to identify the appropriate subproblems to use in order to solve the main problem.

• Recall the weighted interval scheduling problem. Similar approach.

• Let OPT(i) be the optimal solution to the subset sum problem, using a subset of {1, 2, … , i}.

  • Let Oi be its value and hence O is On.

• Should item n be in the optimal solution O or not?

  • If no, then OPT(n-1) = OPT(n)

  • If yes, ?

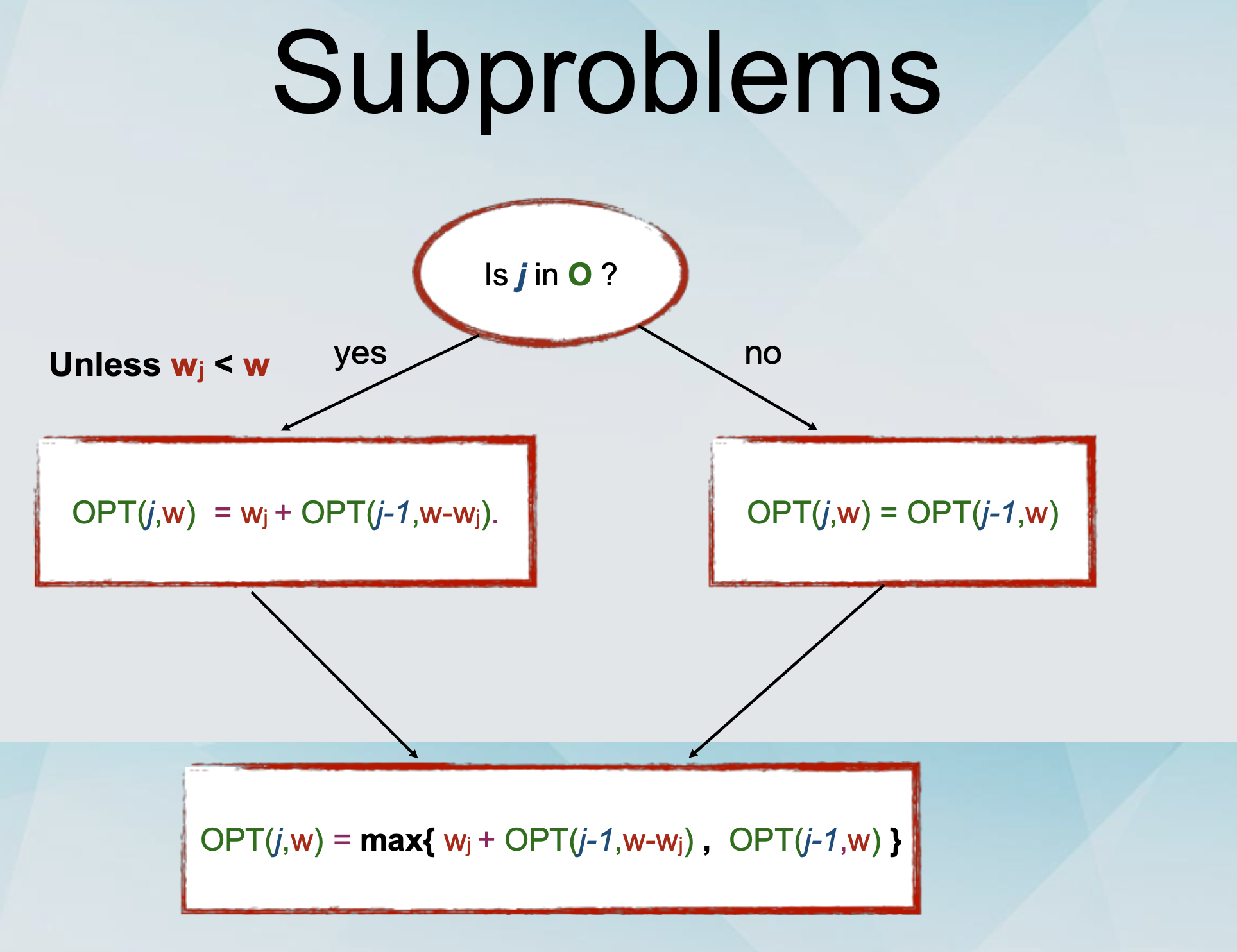
• Subproblems

  • Using this notation, what are we looking for?

  • OPT(n,W)

  • Should item n be in the optimal solution O or not?

  • If no, then OPT(n,W) = OPT(n-1,W).

  • If yes, then OPT(n,W) = wn + OPT(n-1,W-wn).

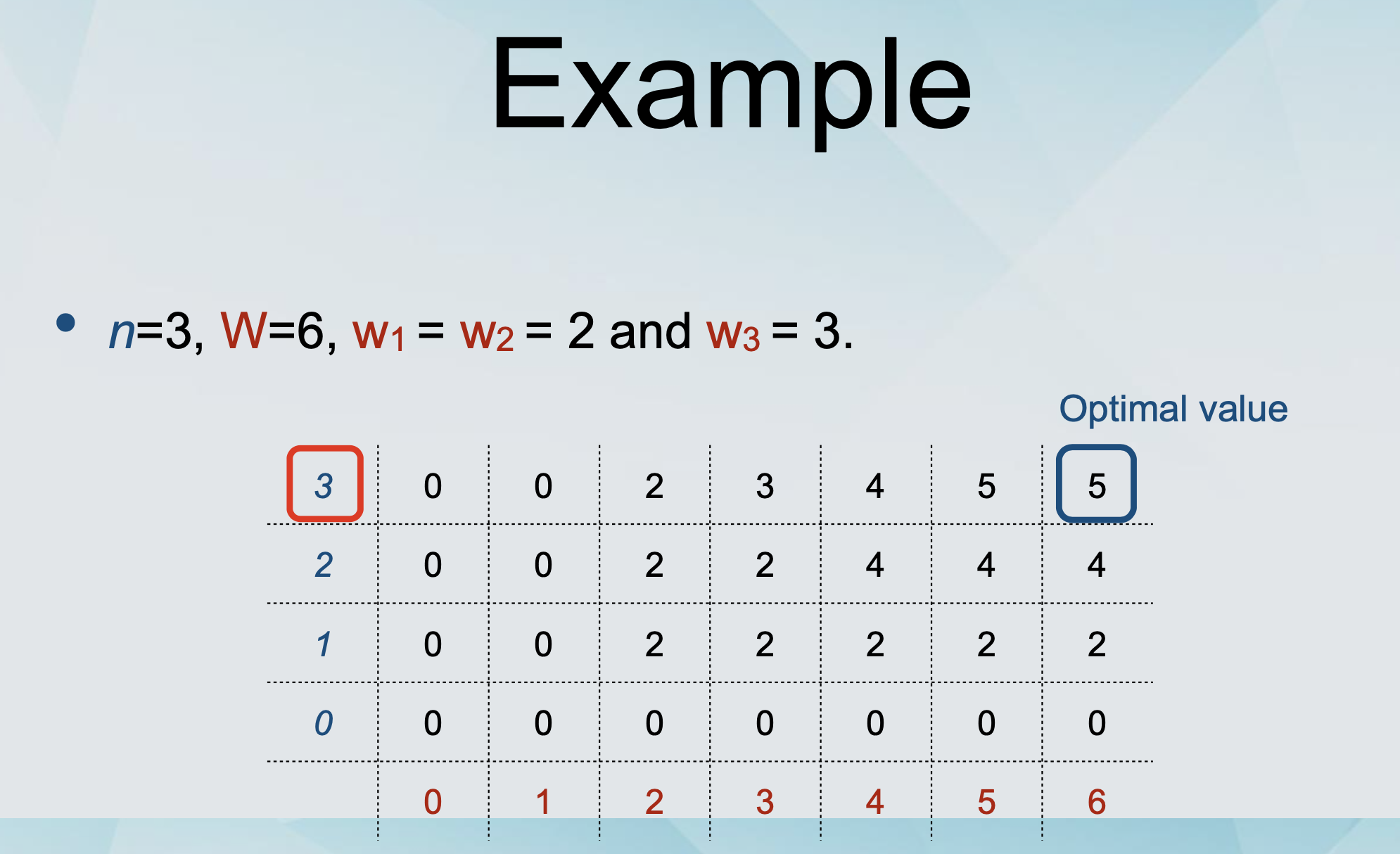
• Example

function subsetSum(arr, maxSum) {
  let res = [[]];
  for (let i = 0; i <= maxSum; i++) {
    res[0].push(0);
  }
  for (let i = 1; i <= arr.length; i++) {
    res[i] = [0];
    for (let j = 0; j <= maxSum; j++) {
      if (arr[i - 1] > j) {
        res[i][j] = res[i - 1][j];
      } else {
        res[i][j] = Math.max(
          res[i - 1][j],
          arr[i - 1] + res[i - 1][j - arr[i - 1]]
        );
      }
    }
  }
  console.log(res);
}

/**
 * 
 * 
3: [0, 0, 2, 3, 4, 5, 5]
2: [0, 0, 2, 2, 4, 4, 4]
1: [0, 0, 2, 2, 2, 2, 2]
0: [0, 0, 0, 0, 0, 0, 0]
 */

• Running Time O(nW)

Knapsack

动态规划三大步骤

1. 定义数组元素的含义，假设定义一个一维数组，那么需要明白 dp[i]代表什么意思
2. 找出数组元素之间的关系式，类似于数学归纳法，当计算 dp[n]时，可以从 dp[n - 2],dp[n - 1]中推导出 dp[n]的值
3. 找出初始值，例如 dp[4] = dp[3] + dp[2]，而 dp[3] = dp[2] + dp[1]。dp[2]和 dp[1]不能再分，这就是初始值

案例

青蛙跳台阶(简单)

描述：一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

1.找出数组含义

dp[n]的含义是：青蛙跳上一个 n 级的台阶总共有多少种跳法

2.找出数组之间的关系式

由题可知，可以选择跳一级，也可以选择跳二级。所以可以得到 dp[n] = dp[n - 1] + dp[n - 2]

3.找出初始值

n 不能为负数，由题可知，dp[1] = 1，dp[0] = 0，dp[2] = 2。

写出算法

  function getMethods(num) {
    let dp = [0, 1, 2];
    if (num <= dp.length) return dp[num]
    for(let i = 3, i < num.length; i++) {
      dp.push(dp[i - 1] + dp[i - 2])
    }

    return dp[num.length - 1]
  }

案例 2：找出到达终点的所有路径

描述：一个机器人位于一个 m x n  网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

dp 定义

表示有多少种方法可以走到 i,j 这个格子

找出数组之间的关系式

dp[i][j] = dp[m][n - 1] + dp[m - 1][n]

定义初始值

dp[0][0] = 1 dp[1][0] = 1 dp[0][1] = 1

写出算法

var dp = [[1, 1], [1]];
for (let i = 0; i < m; i++) {
  for (let j = 0; j < n; j++) {
    if (!dp[i]) dp[i] = [];
    if (!dp[i][j])
      dp[i][j] = (dp[i][j - 1] || 0) + (i - 1 >= 0 ? dp[i - 1][j] : 0);
  }
}
return dp[m - 1][n - 1];

案例 3: 最小路径和

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。 说明：每次只能向下或者向右移动一步。

dp 定义

dp[i][j] 表示路径数字总和的最小值

找出数组之间的关系式

dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]

找出默认值

dp[0][0] = grid[0][0]

题解

// dp[i][j] 表示路径数字总和的最小值
// dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]
// 网格内有默认值
let m = grid.length;
let n = grid[0].length;
let dp = [[grid[0][0]]];
for (let i = 0; i < m; i++) {
  if (!dp[i]) dp[i] = [];
  for (let j = 0; j < n; j++) {
    if (i === 0 && j === 0) continue;
    if (j === 0) {
      dp[i][j] = dp[i - 1][j] + grid[i][j];
    } else if (i === 0) {
      dp[i][j] = dp[i][j - 1] + grid[i][j];
    } else {
      dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
    }
  }
}

return dp[m - 1][n - 1];