Interval Scheduling

The Greedy approach 贪心算法

• The goal is to come up with a global solution. 提出一个全局的解法

• The solution will be built up in small consecutive steps. 会构建连续小步

• For each step, the solution will be the best possible myopically（目光短浅地）, according to some criterion （通过一些准则）.

• Definition:

  • We start by selecting an interval [s(i), f(i)] for some request i.

  • We include this interval in the schedule.

  • This necessarily means that we can not include any other interval that is not compatible with [s(i), f(i)].

  • We will continue with some compatible interval [s(j), f(j)] and repeat the same process.

  • We terminate when there are no more compatible intervals to consider.

• The Greedy Approach

  • Option 1: Choose the available interval that starts earliest.

  • Option 2: Choose the smallest available interval.

  • Option 3: Something more clever.

Interval Scheduling

• A set of requests {1, 2, … , n}.

  • Each request has a starting time s(i) and a finishing time f(i).

  • Alternative view: Every request is an interval [s(i), f(i)].

• Two requests i and j are compatible if their respective intervals do not overlap.

• Goal: Output a schedule which maximises the number of compatible intervals.

Greedy Algorithm for interval scheduling

/**
IntervalScheduling([s(i), f(i)]i=1 to n)
  Let R be the set of requests, let A be empty
  While R is not empty
    Choose a request i with the smallest f(i).
    Add i to A
    Delete all requests from R that are not compatible with request i.
  Return the set A of accepted requests
*/

Arguing for optimality

• Some notation:

  • O is the optimal schedule. Recall, that A is the schedule of the Greedy algorithm.

  • Let i1, i2, … , ik be the order in which the intervals were added to A by the algorithm.

  • Note that |A| = k.

  • Let j1, j2, … , jm be the set of requests in O.

  • Note that |O| = m.

  • We will prove that m=k. (Why is that enough?)

• Let j1, j2, … , jm be the set of requests in O.

  • Assume wlog that this is in order of increasing s(jh).

  • Since O is feasible, this is also in order of increasing f(jh).

• Claim: f(i1) ≤ f(j1)

  • This holds because i1 is chosen to be the interval with the smallest f(ih).

• Claim: f(i1) ≤ f(j1)

  • As i1 is chosen to be the interval with the smallest f(ih).

• Lemma: For all indices r ≤ k, it holds that f(ir) ≤ f(jr)

  • Proof by induction:

    • Base Case (r=1), by Claim.

    • Induction Step. Assume it is true for r-1 i.e. (IH): f(ir-1) ≤ f(jr-1)

    • we will prove it for r.

Induction step proof

Completing the proof

• By contradiction: To the contrary, assume that m > k

• For r=k, the Lemma gives us that f(ik) ≤ f(jk).

• Since m > k , there is an extra request jk+1 in O.

• s(jk+1) > f(jk) ≥ f(ik).

• The greedy algorithm would have continued with jk+1.

Running Time

The running time is O(n log n).

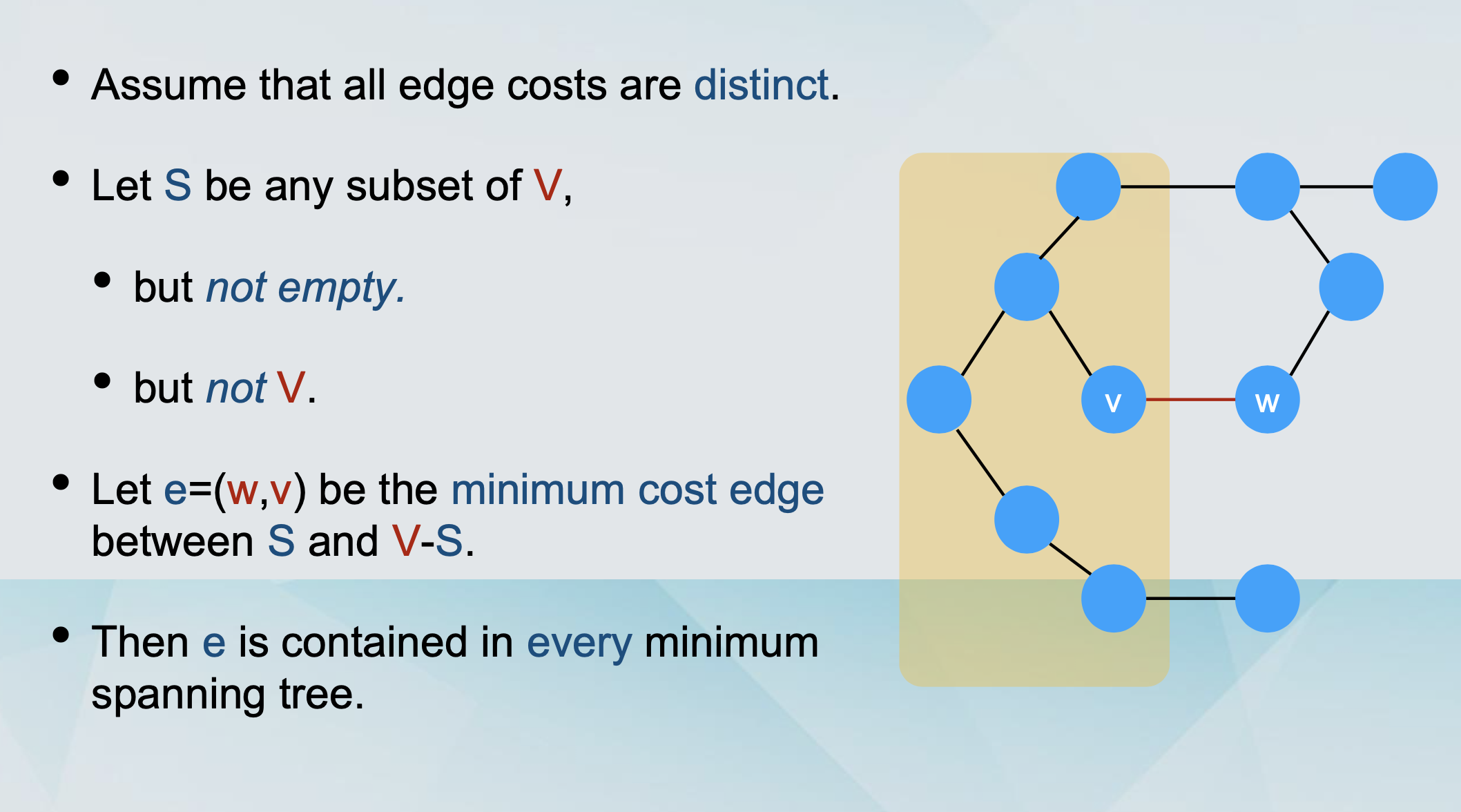
Minimum Spanning Tree 最小生成树

• Consider a connected graph G=(V, E), such that for every edge e=(v,w) of E, there is an associated positive cost ce.

• Goal: Find a subset T of E so that the graph G’=(V, T) is connected and the total cost sum ce is minimised.

Claim: T is a tree

• By definition, (V, T) is connected.

• Suppose that it contained a cycle.

• Let e be an edge on that cycle.

• Take (V, T-{e}).

• This is still connected.

  • All paths that used e can be rerouted through the other direction.

• (V, T-{e}) is a valid solution, and it is cheaper. Contradiction!

Greedy Approach 1 (Kruskal’s Algorithm)

• Start with an empty set of edges T.

• Add one edge to T.

  • Which one?

  • The one with the minimum cost ce.

• We continue like this.

• Do we always add the new edge e to T?

  • Only if we don’t introduce any cycles.

Greedy Approach 2 (Prim’s Algorithm)

• Start with an empty set of edges T.

• Start with a node s.

• Add an edge e=(s,w) to T.

  • Which one?

  • The one with the minimum cost ce.

• We continue like this – growing a set of connected vertices.

  • We only consider edges to neighbours that are not in the spanning tree.

The cut property

Kruskal’s algorithm is optimal

• Consider any edge e=(u, w) that Kruskal’s algorithm adds to the output on some step.

• Let S be the set of nodes reachable from u just before e is added to the output.

• It holds that u is in S and w is in V-S.(Why?)

  • Because otherwise adding e would create a cycle.

• The algorithm has not found any edge crossing S and V-S. (Why?)

  • Such an edge would have been added to the output by the algorithm.

• The edge e must be the cheapest edge crossing S and V-S.

• By the cut property, it belongs to every minimum spanning tree.

Prim’s algorithm is optimal

• In each iteration of the algorithm, there is a set S of nodes which are the nodes of a partial spanning tree.

• An edge is added to “expand” the partial spanning tree, which has the minimum cost.

• This edge has one endpoint in S and one in V-S and has minimum cost.

• So it must be part of every minimum spanning tree.

Greedy Approach 3 (Reverse-Delete Algorithm)

• Start with the full graph G=(V, E).

• Delete an edge from G.

  • Which one?

  • The one with the maximum cost ce.

• We continue like this.

  • Do we always remove the considered edge e from G?

  • As long as we don’t disconnect the graph.

The cycle property

• Assume that all edge costs are distinct.

• Let C be any cycle of G.

• Let e=(w,v) be the maximum cost edge of C.

• Then e is not contained in any minimum spanning tree of G.

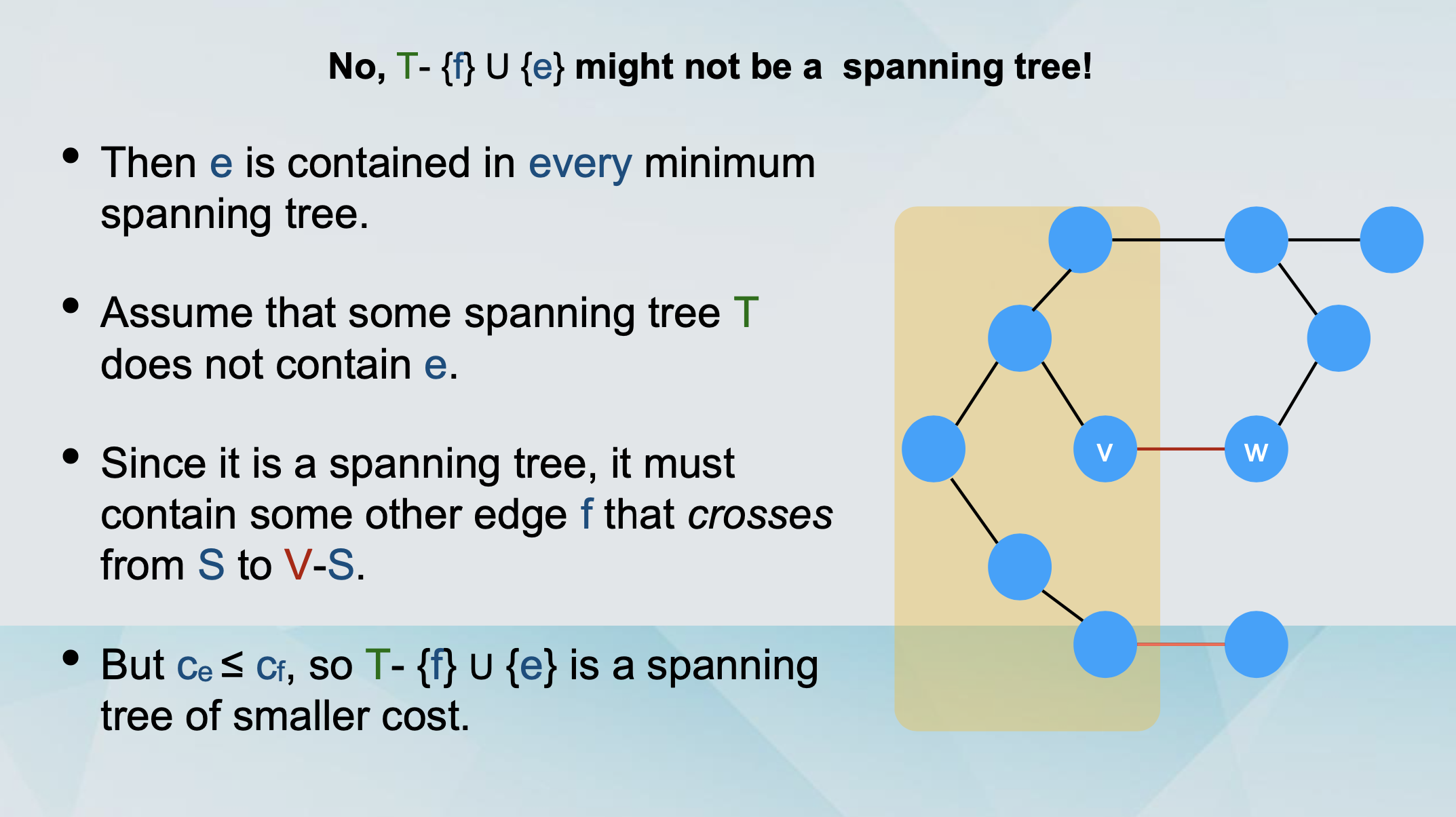
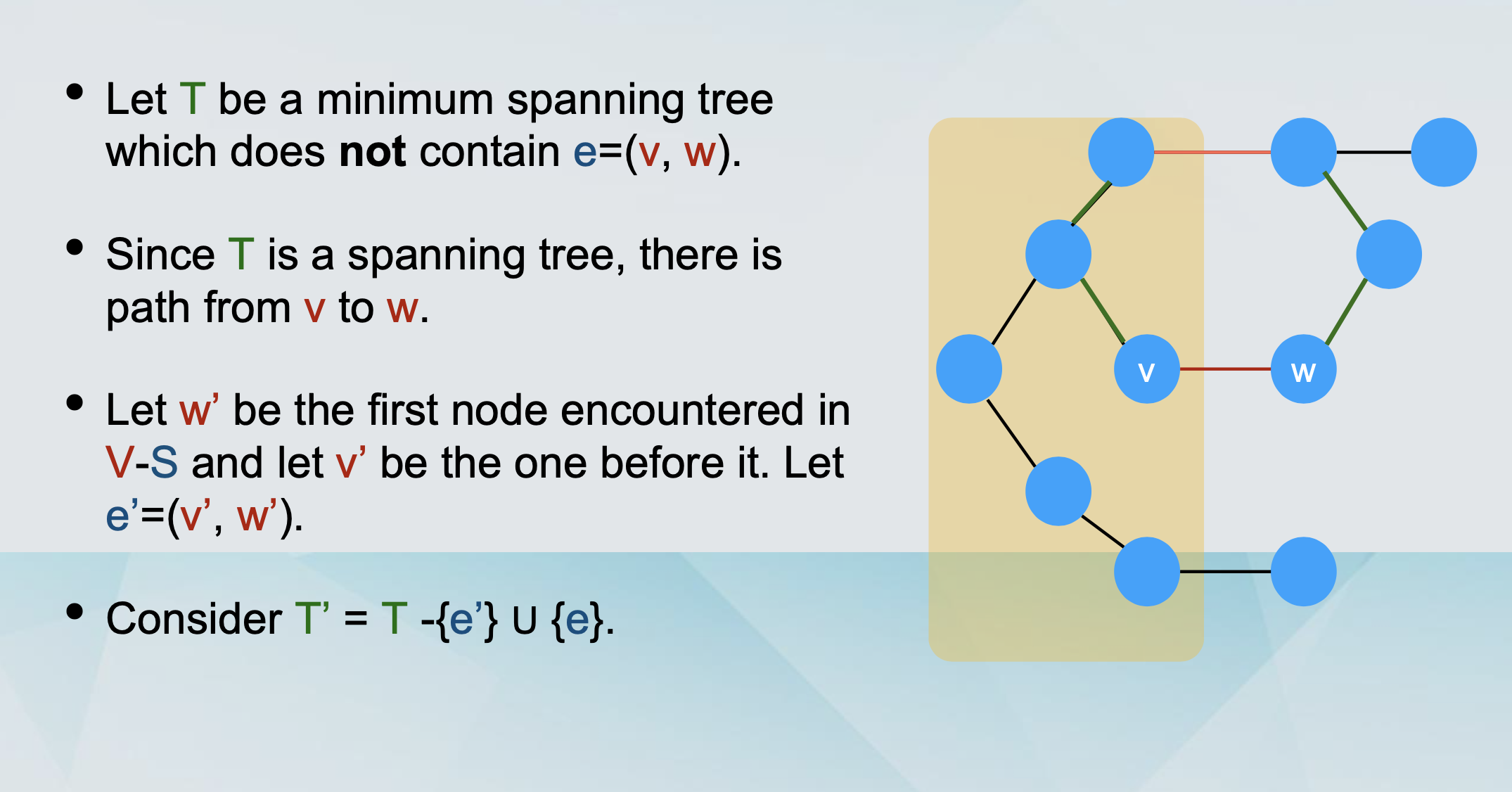
• Let T be a spanning tree that contains e.

• We will show that it does not have minimum cost.

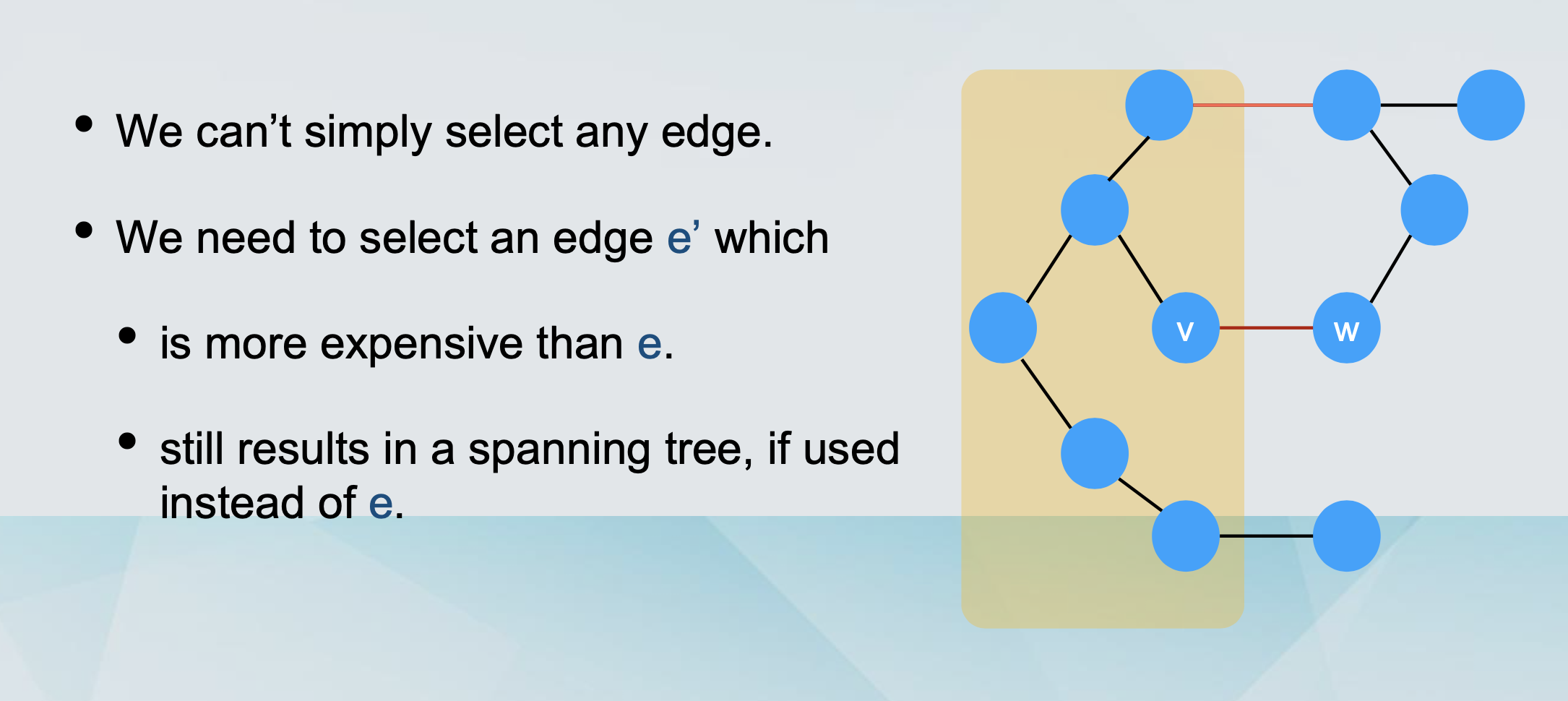
• We will substitute e with another edge e’, resulting in a cheaper spanning tree.

• How to find this edge e’?

• We delete e from T.

• This partitions the nodes into

  • S (containing u).

  • V - S (containing w).

• We follow the other path the cycle from u to w.

• At some point we cross from S to V - S, following edge e’.

• The resulting graph is a tree with smaller cost.

Reverse-Delete is optimal

• Consider any edge e=(v, w) which is removed by Reverse- Delete.

• Just before deleting, it lies on some cycle C.

• It has the maximum cost among edges, so it cannot be part of any minimum spanning tree.

Non-distinct costs

• Take the original instance with non-distinct costs.

• Make the costs distinct by adding small numbers ε to the costs to break ties.

• Obtain a perturbed instance.

• Run the algorithm on the perturbed instance.

• Output the minimum spanning tree T.

• T is a minimum spanning tree on the original instance.

T in the original instance

• Suppose that there was a cheaper spanning tree T* on the original instance.

• If T* contains different edges to T but with the same costs, it is not cheaper than T on the original instance.

• If T contains different edges with different costs, we can make ε small enough to make sure the ones we selected are still cheapest.

Prim’s algorithm running time

• We add nodes to the expanding spanning tree S.

• We need to figure out which node to add next.

• We need to know the attachment cost of each node: a(v) = mine=(u,v):u is in S ce

• Naive solution: For every step run over all candidates.

• O(n2).

Priority Queue

• Maintains

  • A set of elements S.

  • A key key(v) for each element v in S.

• The key denotes the priority of v.

• Operations:

  • Add(v) - with priority key. • Delete(v)

  • Extract_Min(v)

  • Change_key(v)

• The Priority Queue is an abstract data type.

• In reality, we have to implement it with known data structures.

• Many implementations exists, the usual one is with heaps.

• For now:

  • PQ operations can be implemented in O(log n) time.

• PQ solution: Insert the nodes in a PQ, with minus the attachment cost as the keys.

Clustering

Definition of Clustering

• Definition: Given a set U of n elements, a k-clustering of U is a partition of U into non-empty sets C1, …, Ck.

• Definition: The spacing of a k-clustering is the minimum distance between any pair of points in different clusters. // 不同集合之间的最小距离

• Goal: Among all possible k-clusterings, find one with the maximum possible spacing.

In greedy algorithm

• Pick two objects pi and pj with the smallest distance d(pi,pj).

• Connect them with an edge e=(pi,pj).

• Continue like this until we obtain k clusters.

• If the edge e under consideration connects two objects pi and pj already in the same component, skip it.

Kruskal’s algorithm

• Pick an edge (pi, pj) with the smallest cost d(pi,pj).

• Include the edge in the output.

• Stop before including the last k-1 edges.

  • i.e., in the end, remove the k-1 most expensive edges.

• If the edge e under consideration introduces a cycle, then skip it.

• Lemma: Let C1, C2, … , Ck be the k connected components formed by deleting the k-1 most expensive edges from a minimum spanning tree T. // 生成一个最小生成树需要删除 k - 1 条最 expensive 的边

• Proof of the Lemma

  • Let C’ = {C’1, C’2, … , C’k} be any other k-clustering.

  • By other, there exists a cluster Cr of C which is not contained in any cluster C’s of C’.

  • This means that there exist points pi, pj in Cr that belong to different clusters in C’.

  • Let C’i and C’j denote these clusters respectively.