Profit Maximization

• Goal: Maximize the profit.

• Allocation Algorithm: Give the object to the player with the highest bid.

• Payment Scheme: The winner pays an amount equal to the second highest bid.

Bayesian Setting

• Sometimes it makes sense to assume that some partial information is known. （部分数据已知）

• Assume that the valuations come from a known probability distribution. The distribution is common knowledge! （估值来自一个概率分布， 这个分布是一个 knowledge）

• Assume that you have a single player with v1∼U[0,1].

• What sort of mechanism would we devise to maximize the expected revenue?

  • We post a price p
  • if v≥ p we give the item to the bidder at price p
  • if v < p we keep the item

• What is the optimal price p?

The optimal price is p=1/2 and gives us expected revenue 1/4.

Second Price Auction

• Assume that there are two players with v1,v2∼U[0,1].

• What is the expected revenue that we get from the second price auction?

` - Truthful auction: we consider b1(v1)=v1, b2(v2)=v2.

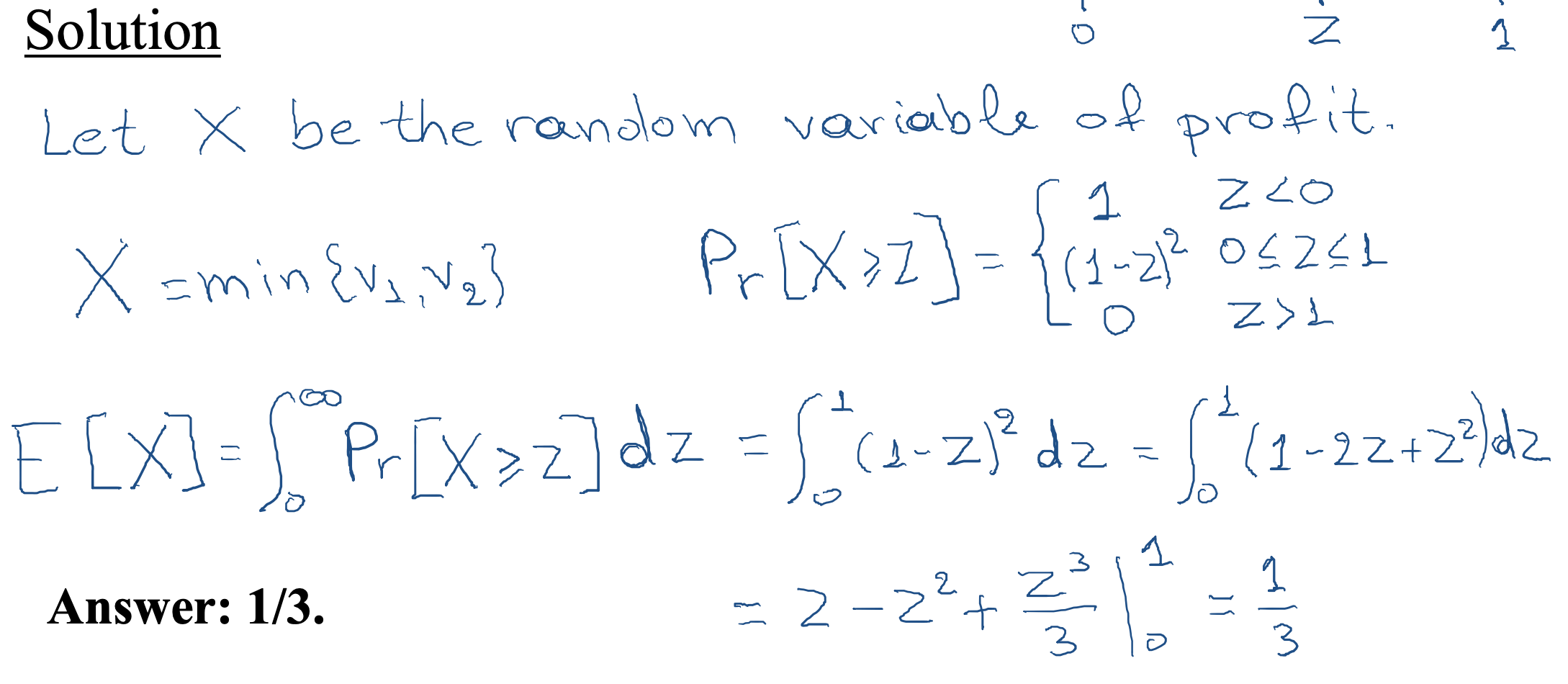
• Answer: 1/3.

First Price Auction

• Assume that there are two players with v1,v2∼U[0,1].

• First price auction is not truthful.

• What is a Bayesian Nash equilibrium for the first price auction?

  • Answer: b1(v1) = v1/2, b2(v2) = v2/2. (CANVAS)

• Notice that the social welfare is maximized in equilibrium, i.e. we assign the item to the highest true value!

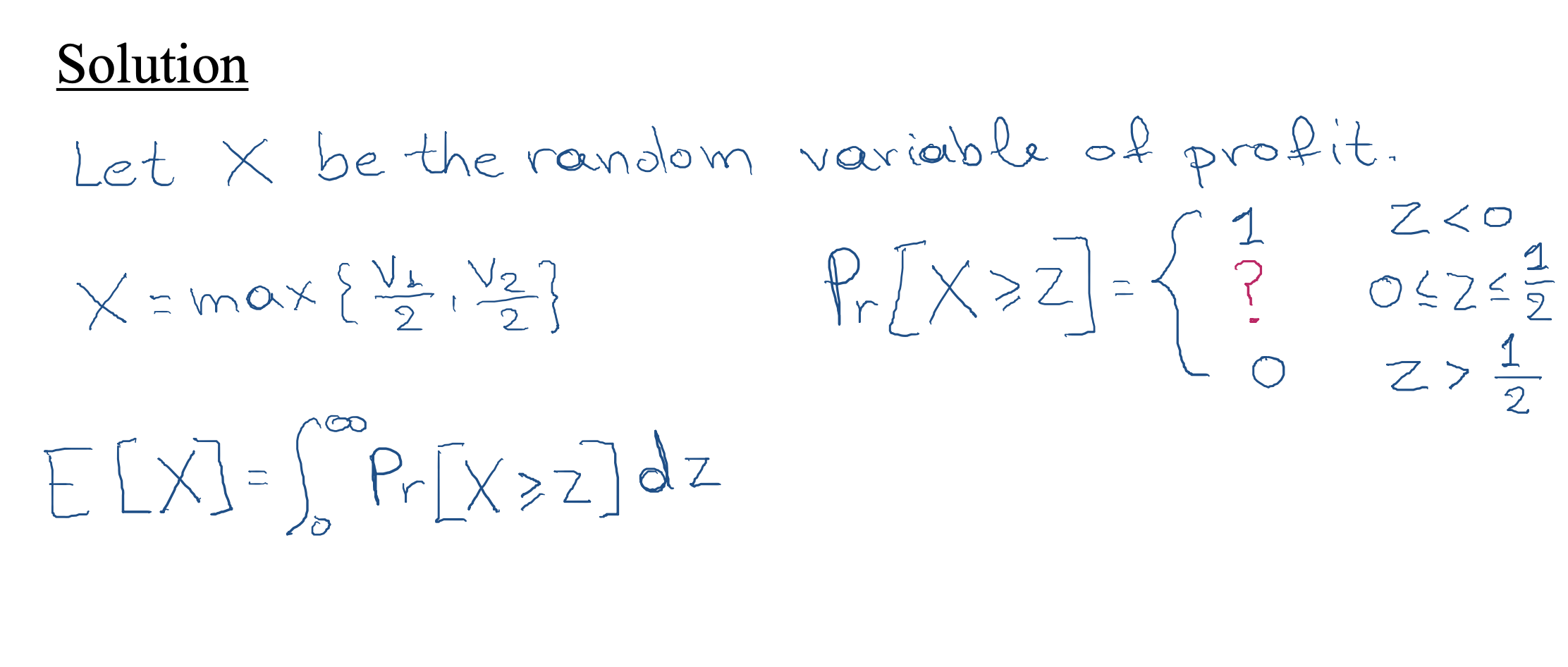
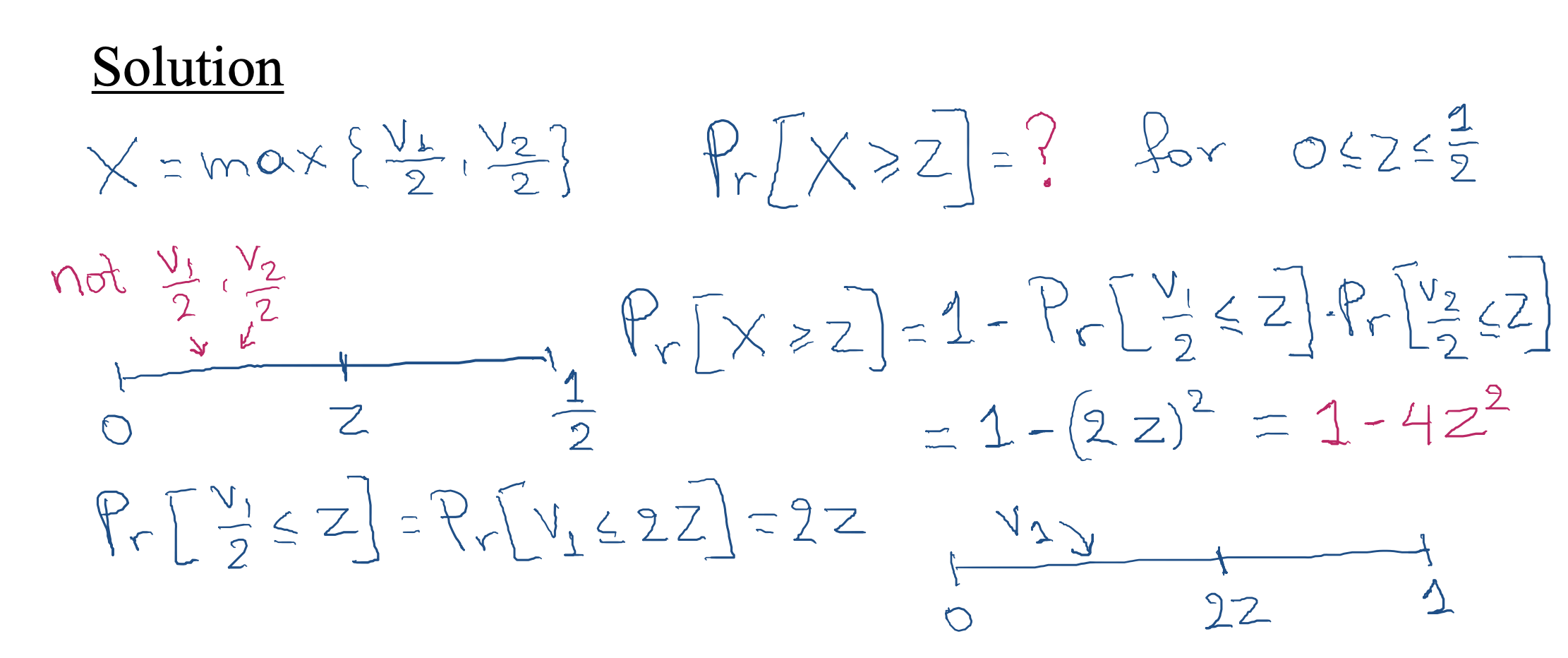
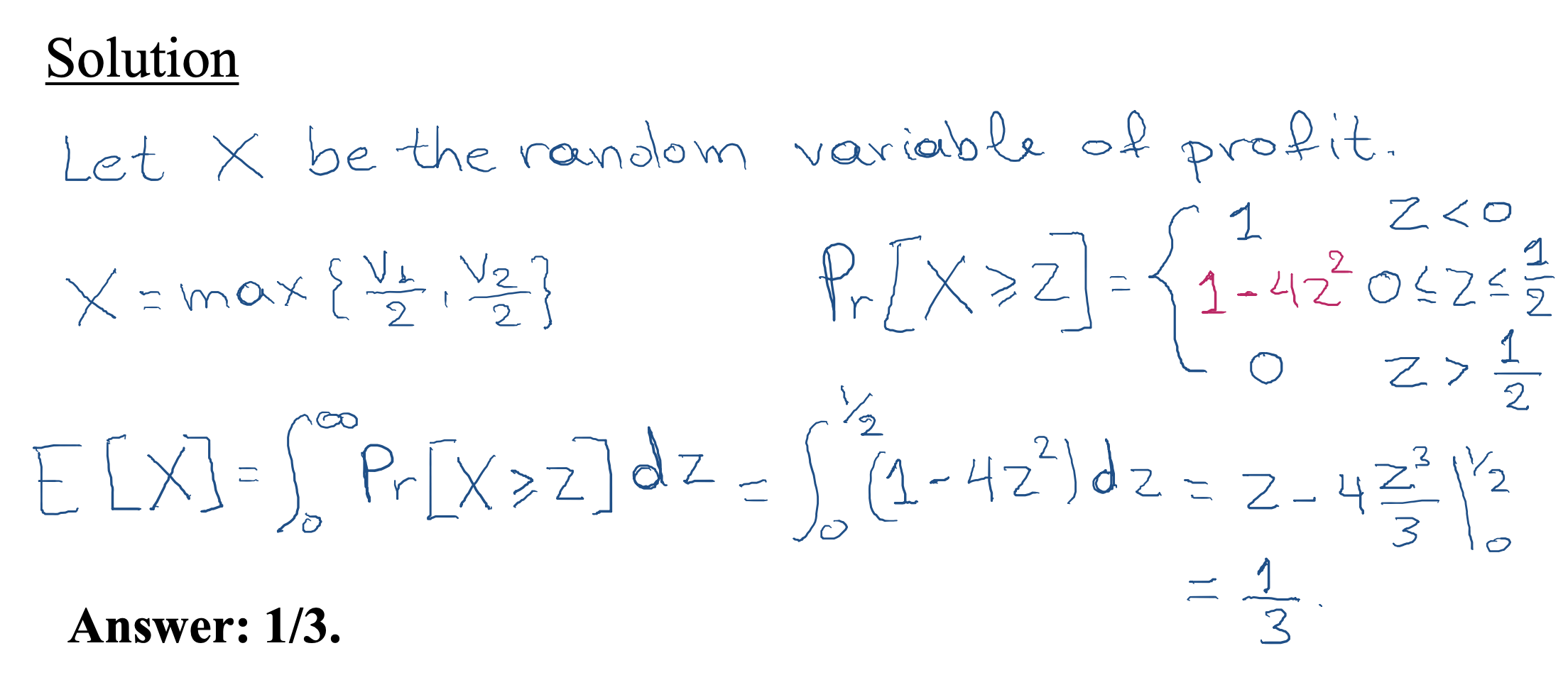
Revenue Equivalence Principle

All single-item auctions that allocate (in equilibrium) the item to the player with highest value and in which losers pay 0, will have identical expected revenue.

• Assume that there are two players with v1,v2∼U[0,1].

• Can we improve upon the 1/3 expected revenue in a truthful way?

• Vickrey Auction with Reserve Price 1/2.

  • if v1 < 1/2 and v2 < 1/2 we do not allocate the item

  • if v1 < 1/2 and v2 ≥ 1/2 we allocate the item to bidder 2 for price of 1/2

  • if v1 ≥ 1/2 and v2 < 1/2 we allocate the item to bidder 1 for price of 1/2

  • if v1 ≥ 1/2 and v2 ≥ 1/2 we allocate the item to the highest bidder and charge him the second highest bid.

• Is this auction truthful? Yes

  • Add a dummy bidder (auctioneer) with value 1⁄2. Run Vickrey auction.

  • This auction is an affine maximizer.

• What is the expected revenue that we get from this auction?

  • Answer: 5/12 > 4/12 = 1/3.

• What is the highest expected revenue that we get from this auction?

  

  

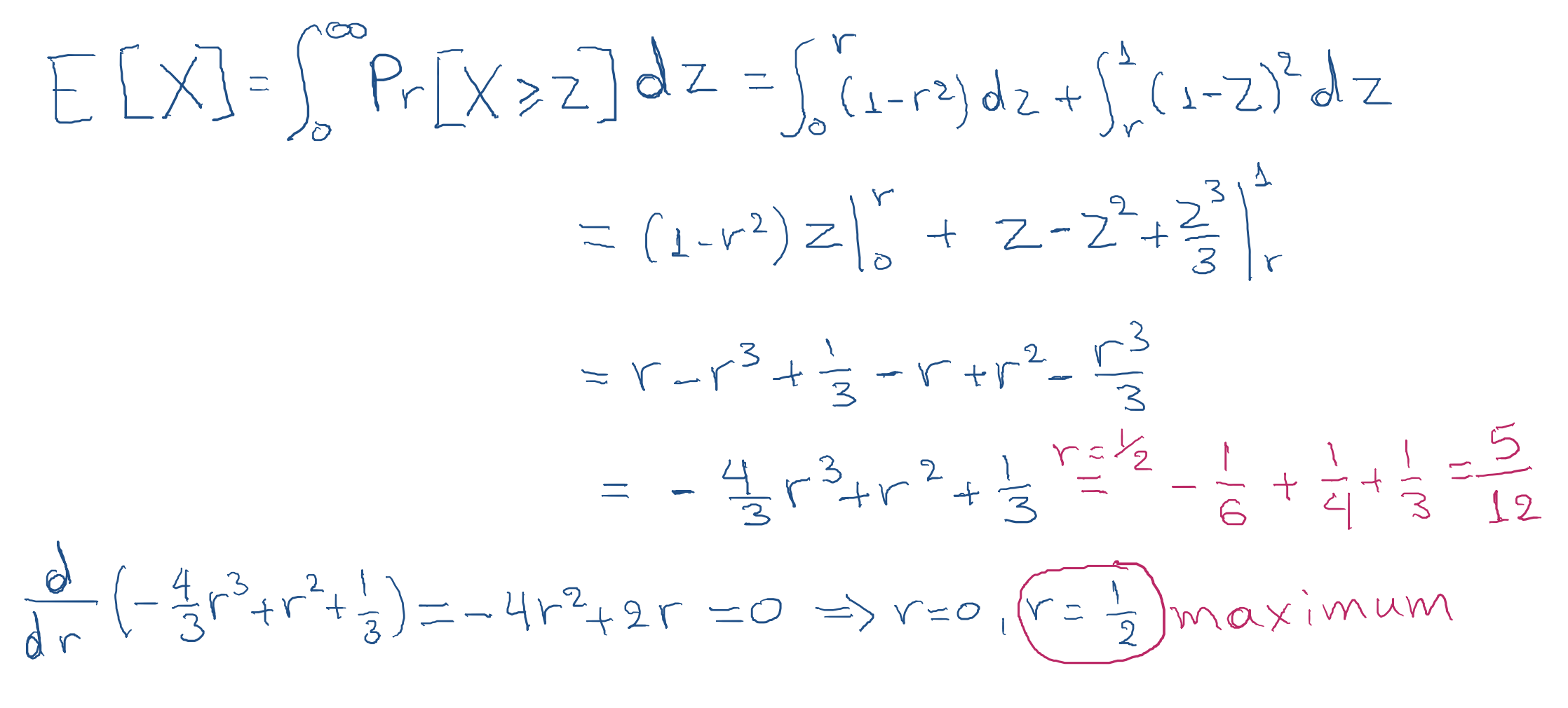
  • Answer: 5/12 (r=1/2)

Single item auction

• Definition

  • Assume that there are n bidders with vi ∈ [0,h].

  • Mechanism M(x, p1, … , pn)

  • Input: b=(b1,…,bn) the vector of declarations

  • Output: x(b) allocation function

    1. xi(b)=1 if i gets the item

    2. xi(b)=0 if i does not get the item

  • Output: p1(b),…,pn(b): payment functions

  • The utility of player i if his true value is vi but he reports bi is

    ui(bi,b-i;vi)= vi⋅xi(bi,b-i)-pi(bi,b-i)

• Notice that player i’s valuation is a single-parameter.

• A mechanism is truthful if for every i, bi,vi,b-i

  ui(vi,b-i;vi) ≥ ui(bi,b-i;vi)

  vi⋅xi(vi,b-i)-pi(vi,b-i) ≥ vi⋅xi(bi,b-i)-pi(bi,b-i)

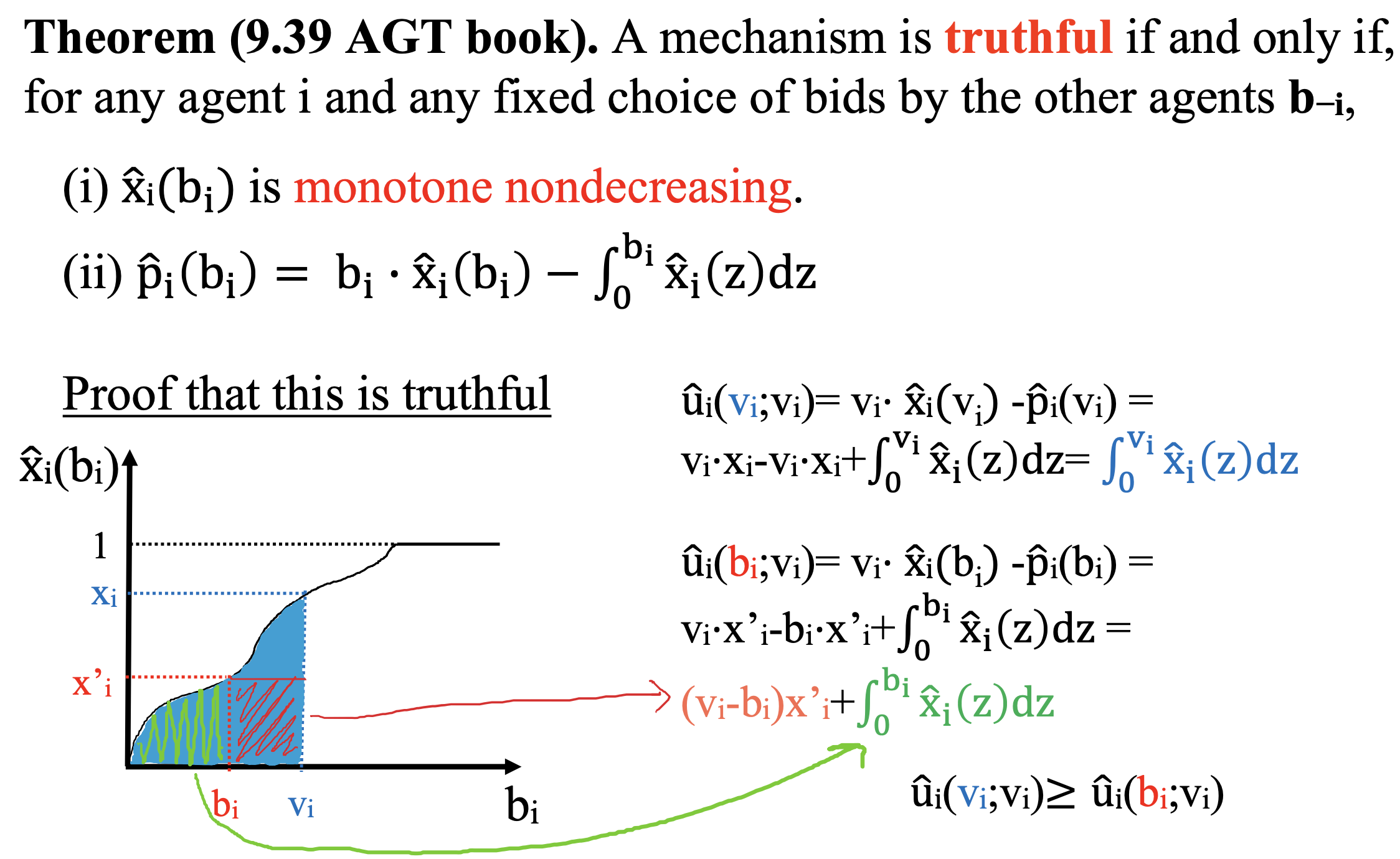
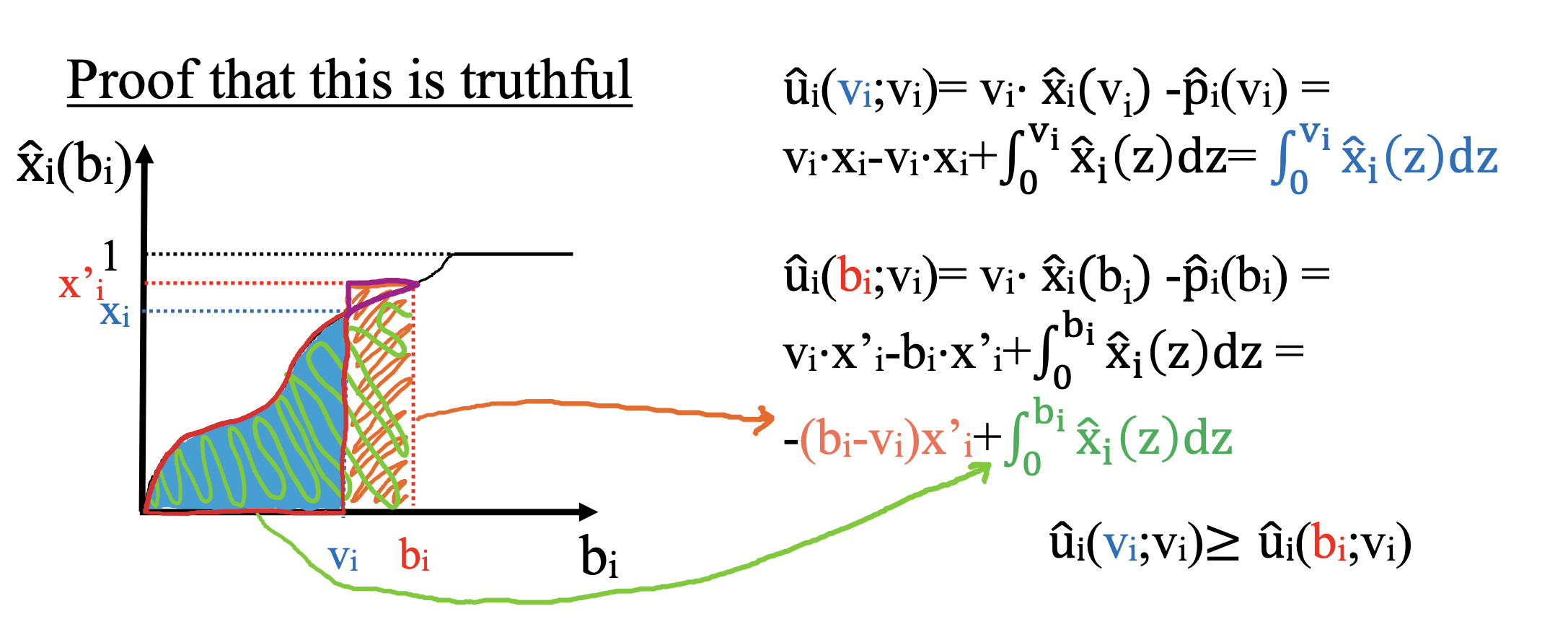
• Theorem (9.39 AGT book). A mechanism is truthful if and only if, for any agent i and any fixed choice of bids by the other agents b−i,

  

• Example:

  

  

Virtual valuations

• Definition. The virtual valuation of agent i with valuation vi is

  

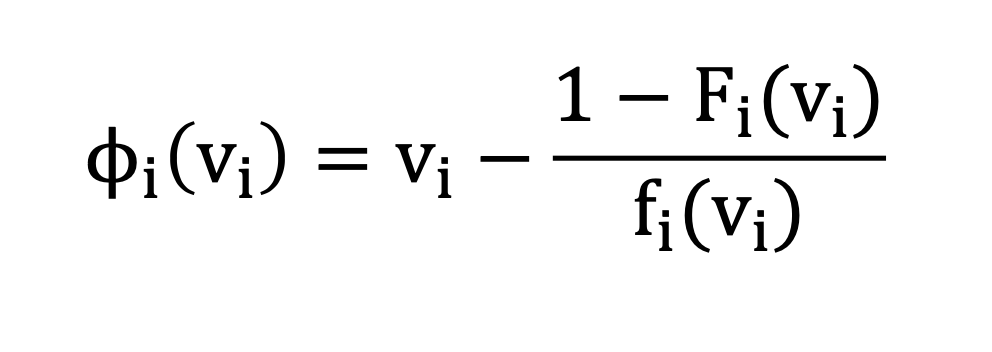
• Definition. Given valuations, vi , and corresponding virtual valuations, φi(vi), the virtual surplus (social welfare) of allocation x is

  

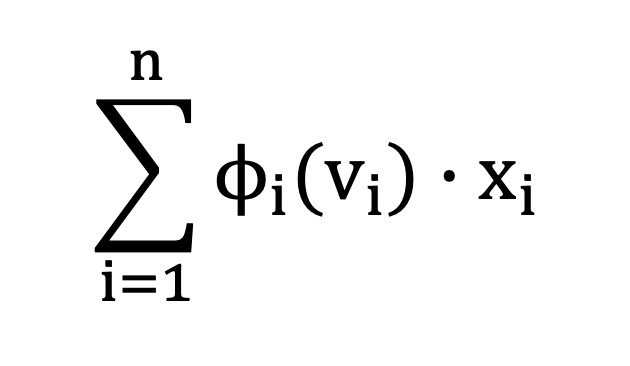
• Theorem. The expected profit of any truthful mechanism, M, is equal to its expected virtual surplus

  • example

  

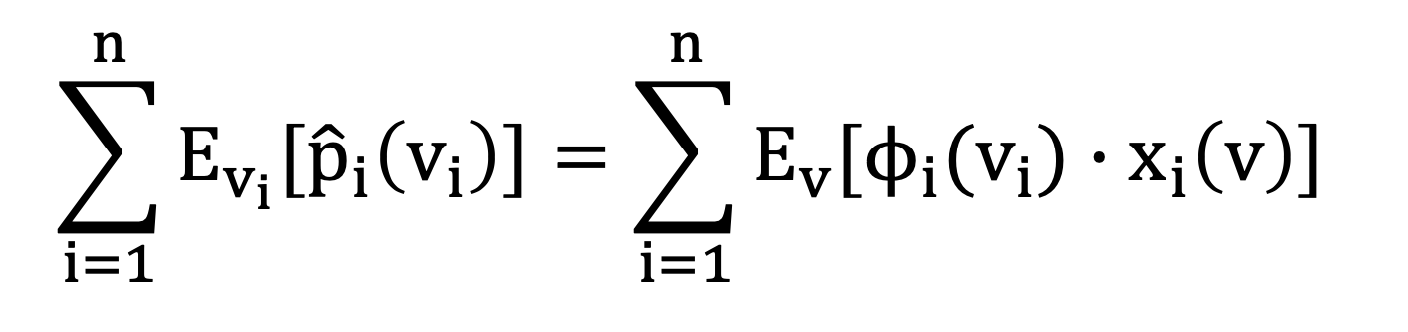
• Lemma. Consider any truthful mechanism and fix the bids v−i of all bidders except for bidder i. The expected payment of a bidder i satisfies:

  

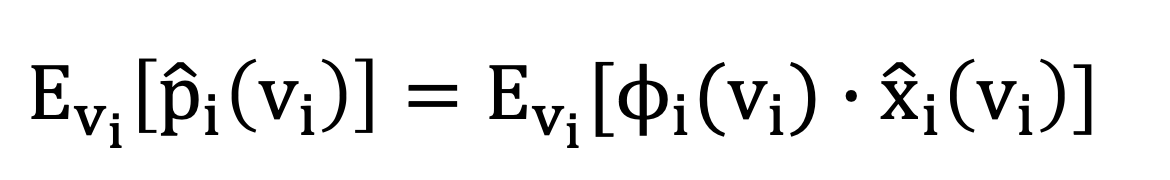
  • proof:

    

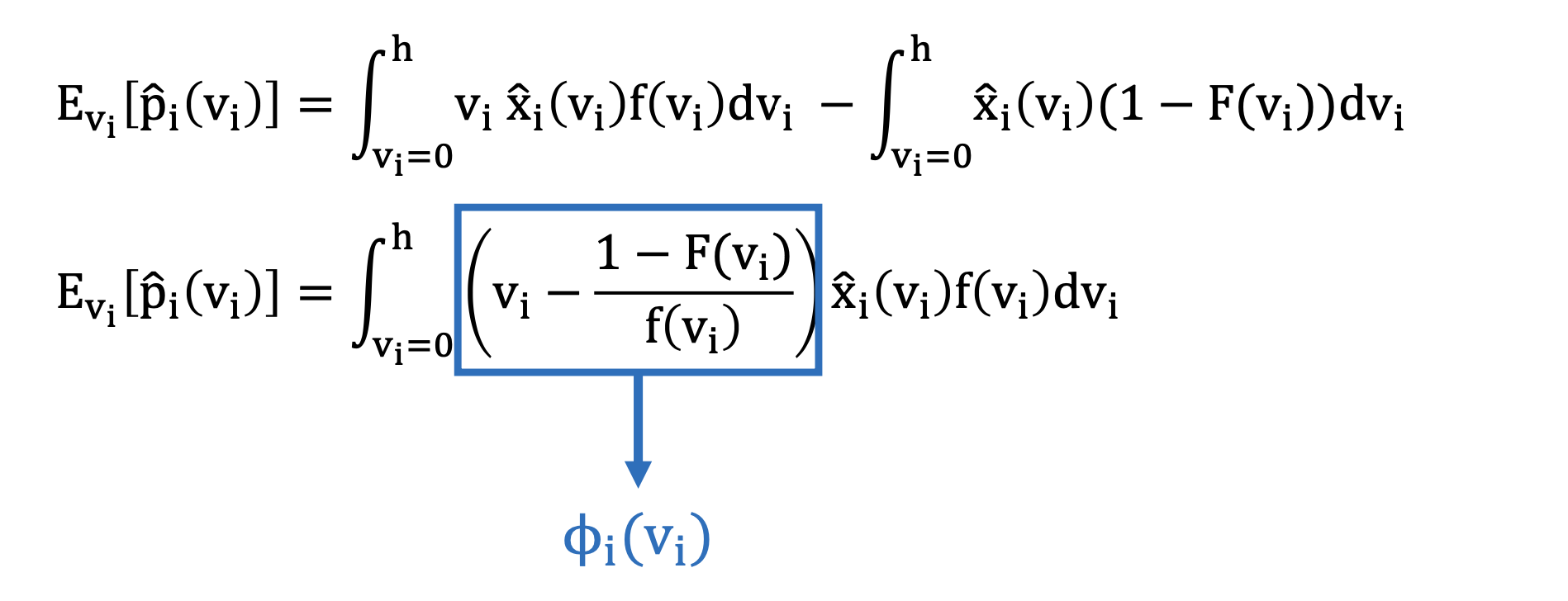
• Lemma. Virtual surplus maximization is truthful if and only if, for all i, φi(vi) is monotone nondecreasing in vi.

  

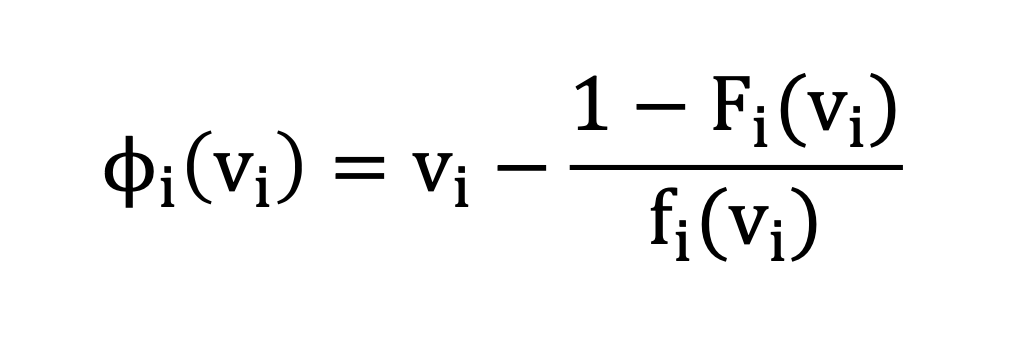
Myerson’s Optimal Mechanism

• Definition: MyeF(b)

  1. Given the bids b and F, compute “virtual bids”: b′i = φi(bi).

  2. Run VCG on the virtual bids b′ to get x′ and p′

  3. Output x = x′ and p with pi = φ−1i (p′i) (upon winning).

• MyeF(v1,v2): Vickrey Auction with Reserve Price 1/2

• Q: Can we do better?

  • No, Mayerson’s mechanism is optimal.