Combinatorial Auctions (1)

Single Item Auction

• Goal: Give the object to the player with maximum value.
• In a way that cannot be strategically manipulated

Multiunit Auctions

• Definition:

  • Allocation Algorithm: Give the k objects to the k highest bidders.

  • Payment Scheme: The winners pay an amount equal to the k+1st highest bid.

Example Combinatorial Valuations

• Problem Statement

  • A set M of m indivisible items M={1,…,m}

  • A set N of n bidders N={1,…,n}

  • Bidders have preferences over subsets (bundles) of items A valuation is a real valued function for every subset S of items v(S) is the value the bidder obtains if he receives the bundle S

  • free disposal: monotone v(S)≤v(T) if S⊆T

  • normalized: v(∅)=0

• Example

  

Roberts Theorem

• Theorem (Roberts) If |A| ≥ 3, f is onto A, Vi = RA for every i, and (f, p1, . . . , pn) is incentive compatible then f is an affine maximizer.

Valuations

Take S,T with S∩T=∅

• v is additive if v(S∪T)=v(S)+v(T)

Generally, v is not necessarily additive

• S,T are Complements: v(S∪T) > v(S)+v(T) (Superadditive)

v(pair of shoes) > v(left shoe)+v(right shoe)

-S,T are Substitutes: v(S∪T) < v(S)+v(T) (Subadditive) v({margarine,butter}) < v(margarine)+v(butter)

E.g. Multiunit Auctions (Unit demand valuation)

Utility

• The utility is v(S)-p

• No externalities: the bidder cares only about the set of items he receives and not about how the rest of the items are allocated

Allocation

Social Welfare in Auctions

• Example – Maximize SW

• Goals

  1. Maximize social welfare

  2. Maximize revenue

  3. Minimize envy

• Challenges

  1. Computational Complexity:
  • The allocation problem is computationally hard even for special cases.
  • How do we handle this?
  2. Representation and Communication:

  • The valuation functions are exponential size objects. •How can we even represent them?

  • How can we transfer enough information to the auctioneer so that a reasonable allocation can be found?

  3. Strategies:
  • Can we design incentive-compatible mechanisms?

• Applications

  • Spectrum Auctions: Government sells licences/rights to transmit signals of specific electromagnetic wavelengths

  • Transportation: “Reverse” or procurement auction.

  • A commercial company (buyer) needs to buy transportation services for a large number of routes from various transportation providers (sellers).

  • Each supplier has a value for every bundle of routes.

Single-Minded Bidders

• Definition

  1. A valuation v is called single-minded if there exists a bundle of items S∗ and a value v∗ ∈ R+ such that v(S) = v∗ for all S ⊇ S∗, and v(S) = 0 for all other S.

  2. A single-minded bid is the pair (S∗, v∗).

• Example

• Known valuations

• The allocation problem

Computational Complexity

• Proposition. The allocation problem among single-minded bidders is NP-hard.

• More precisely, the decision problem of whether the optimal allocation has social welfare of at least k (where k is an additional part of the input) is NP-complete.

Approximation

• Approximate allocation (single-minded)

• Proposition. Approximating the optimal allocation among single-minded bidders to within a factor better than m^1/2−ε is NP-hard.

• Running the VCG may need exponential time!

• Even if we knew the valuations, we couldn’t be able to approximate the optimum social welfare by a factor better than m^1/2−ε in polynomial time.

Incentive-Compatible Mechanism

• Compute the optimal allocation and charge VCG payments

  This is incentive-compatible

  Not computationally efficient

• Take an approximate solution and charge VCG payments?

  The VCG payments work only with exact optimization.

The Greedy Mechanism for Single-Minded Bidders

• Example

• Theorem. The Greedy mechanism is efficiently computable, incentive compatible and produces a m^1/2 approximation of the optimal social welfare.

Incentive Compatibility

• Proof Outline

  • First, we will show that a larger class of mechanisms are truthful.

  • Then, we will show that Greedy belongs to this class, and therefore is truthful.

Monotonicity

• A bidder who wins with bid (S∗i , v∗i) keeps winning for any v′i ≥v∗i andforanyS′i ⊆S∗i (for any fixed settings of the other bids).

• Example:

  

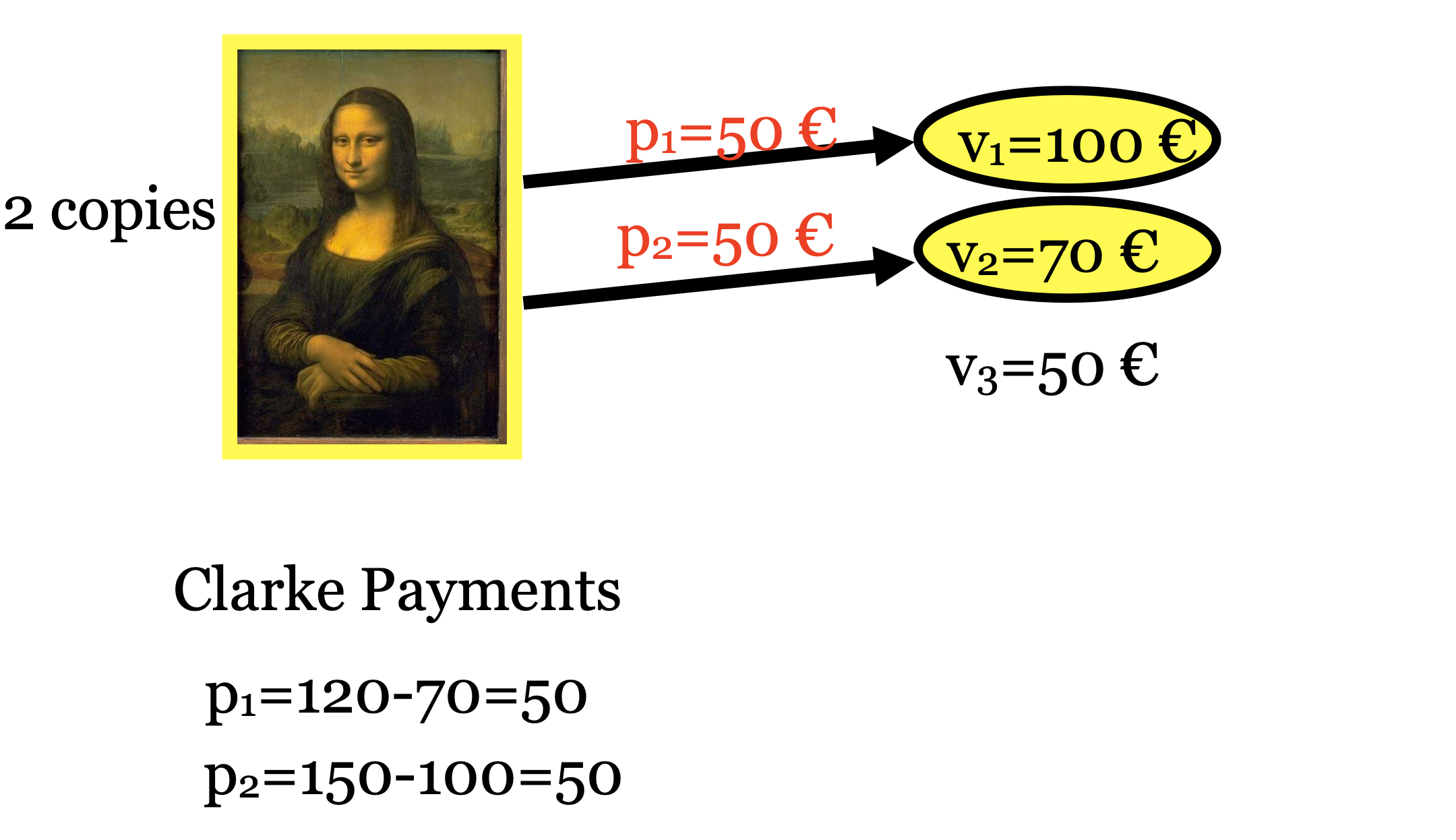
Critical Payments

• Critical Payment: A bidder who wins pays the minimum value needed for winning: the infimum of all values v′i such that (S∗i , v′i ) still wins.

• Example:

  

Incentive Compatibility

• Lemma. A mechanism for single-minded bidders, in which losers pay 0, is incentive compatible if and only if it is Monotone and uses Critical Payment.

• The Greedy is a mechanism for single-minded bidders, in which losers pay 0, and it is Monotone and uses Critical Payment. Therefore, it is incentive compatible.

Approximation

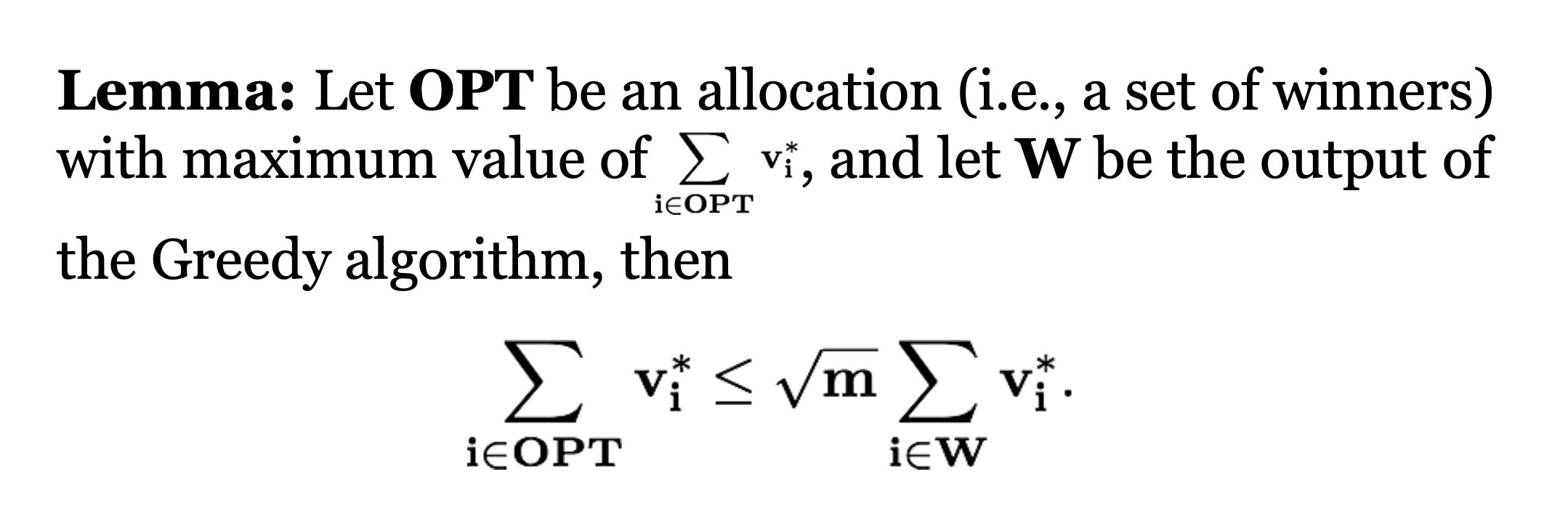
Part2

Other Valuations

Iterative Auctions

The Query Model

• Indirect way of sending information about the valuations

• The auction protocol repeatedly interacts with the different bidders, aiming to adaptively elicit enough information about the bidders’ preferences as to be able to find a good (optimal or close to optimal) allocation.

Advantages

• Reduces the amount of information transferred
• Preserve some privacy about the valuations
• Makes bidder’s life easier (concentrates on the mechanisms queries) Bidder is a “Black-Box” represented by an oracle

Query Model

• The auctioneer presents a bundle S, the bidder reports his value v(S) for this bundle.

Subadditive Valuations

• v(S U T) <= v(S) + v(T)

• Can we design incentive compatible mechanisms that approximate the optimal social welfare?

Affine Maximizers

• Example 1

  A’={all the assignments that assign only the first item to a player} Optimize over A’, charge the VCG payments.

  • It is incentive compatible as an affine maximizer. - Poor approximation ratio.

  	a	b	{a, b}
  v1	ε	1	1
  v2	ε	1	1

  • SW(ALG) = ε

  • SW(OPT) = 1+ε

  • Approximation ratio = SW(OPT)/SW(ALG) = (1+ε)/ε

• Example 2

  	i1	i2	M
  v1	1	1	1
  v2	1	1	1
  vn	1	1	1

  • SW(ALG) = 1

  • SW(OPT) = n

  • Approximation ratio = SW(OPT)/SW(ALG) = n

• Exact optimization in A’ gives good approximation for A

(DNS) Mechanism for SA valuations

i) For each bidder i=1,…, n do:

1. Query bidder i for the set M={1,…,m}

2. For each item j=1,…,m do: Query bidder i for the item j

ii) Construct a bipartite graph G=(N,M,E)

1. a vertex bi for every player i 2) a vertex aj for every item j

2. E=(bi,aj)

3. w(bi,aj)=vi(j)

iii) Compute a maximum weighted matching P of G

iv) Find the bidder i*∈ arg maxi vi(M)

v) Return the assignment with maximum S.W. among iii) and iv)

• example

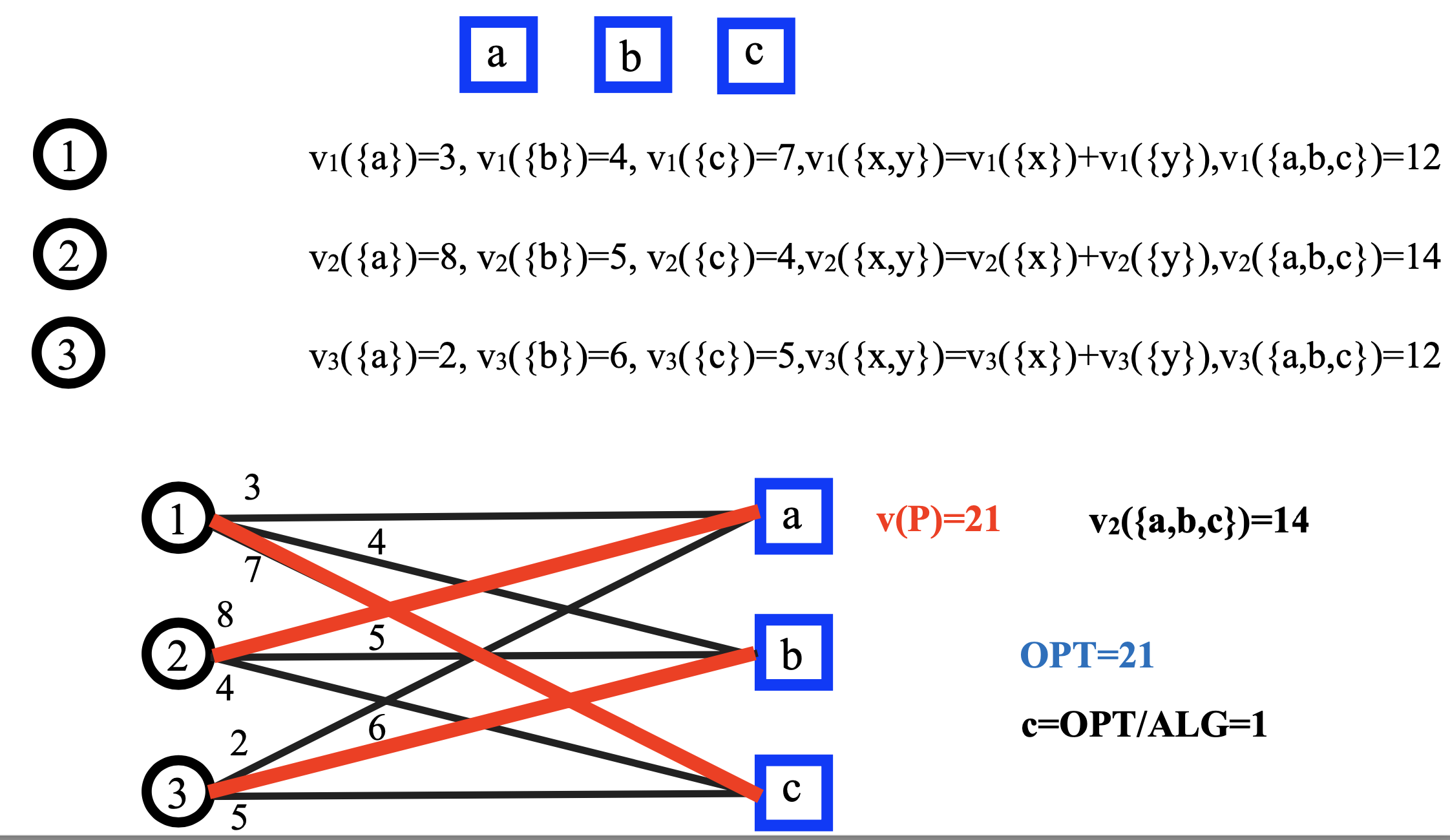
• example 2

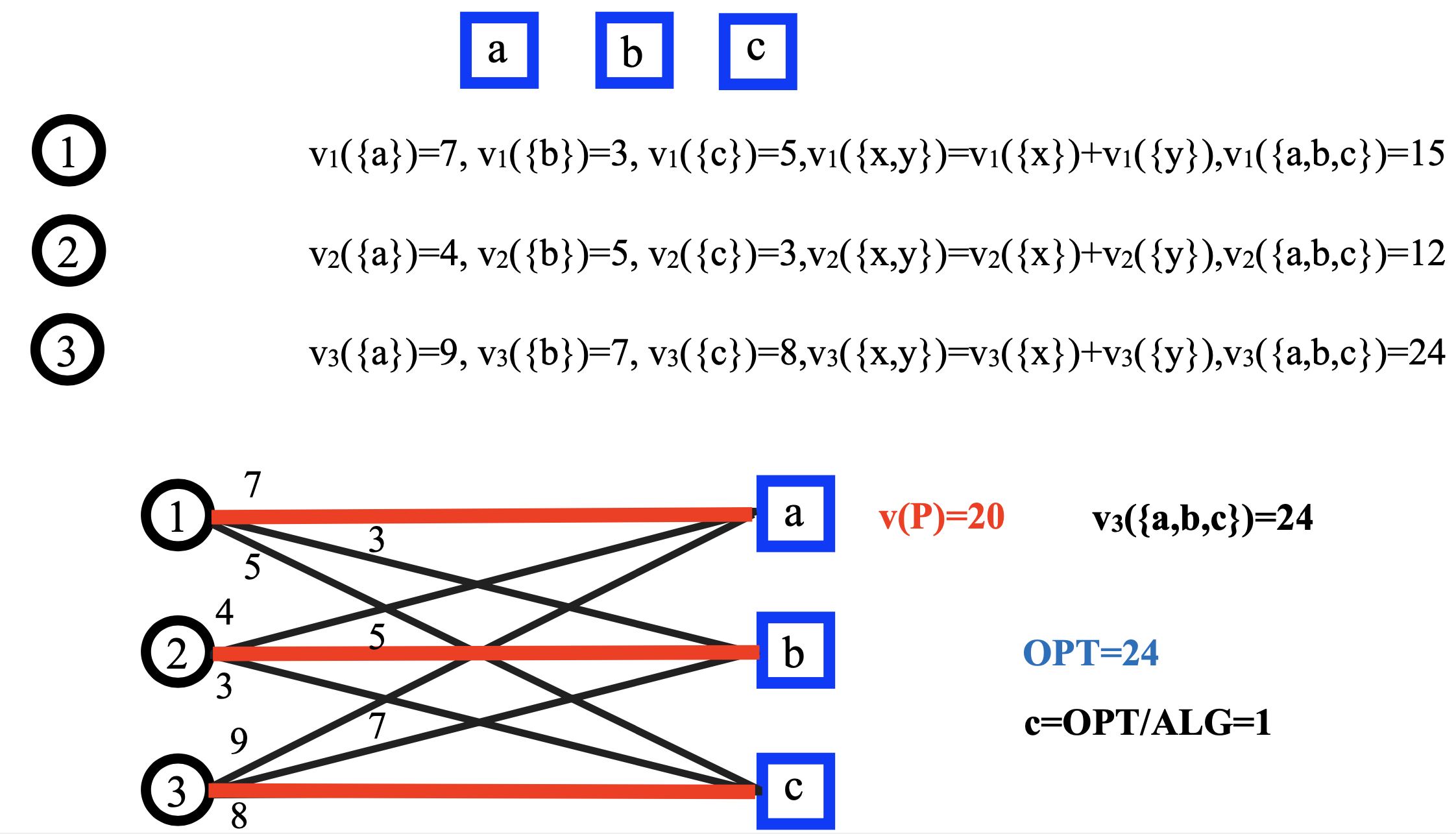
• example 3

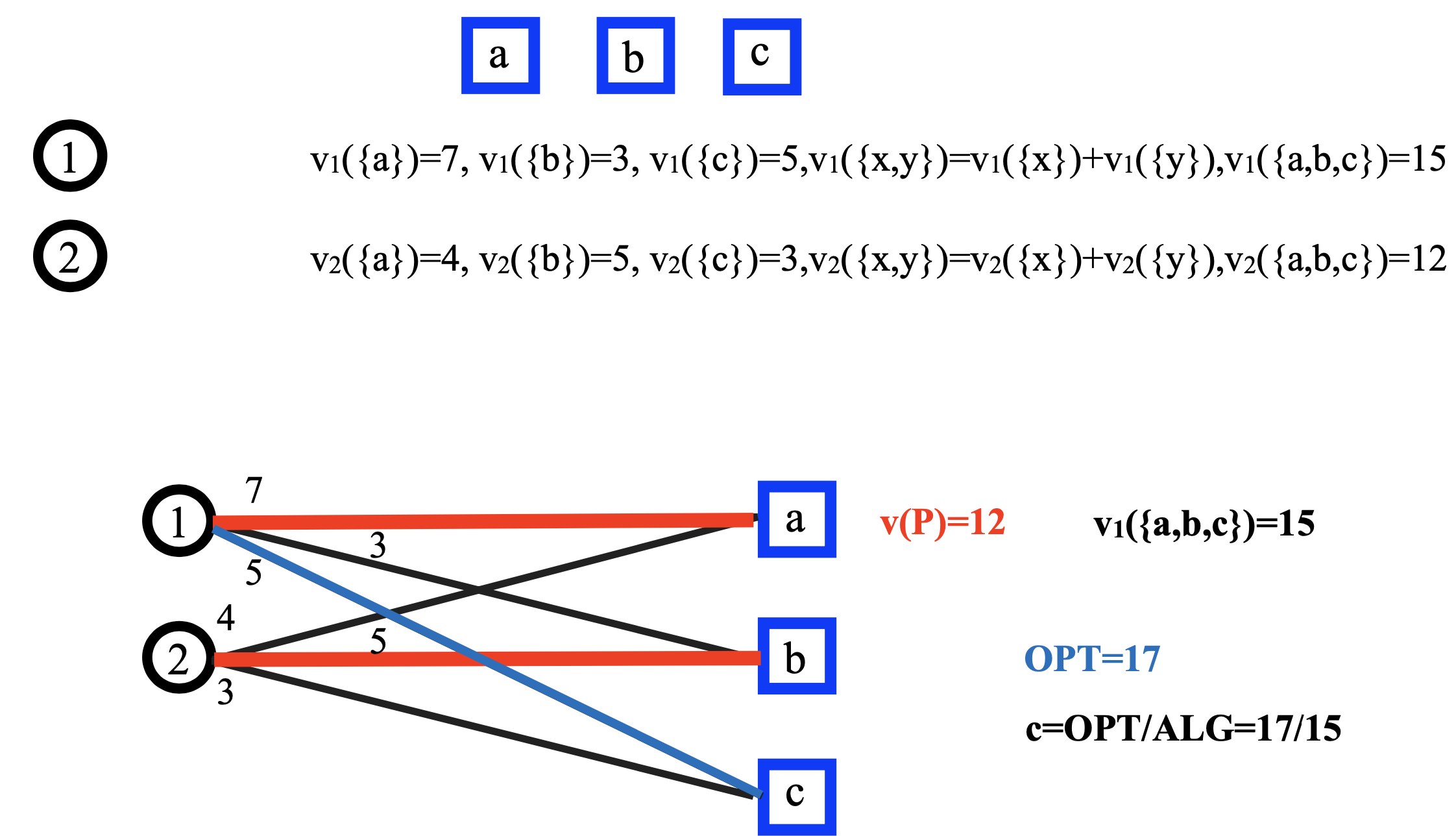
• Theorem. The DNS mechanism is efficiently computable, incentive compatible and produces a O(m1/2) approximation of the optimal social welfare for subadditive valuations.

Item Bidding Auctions

• Item-bidding or simultaneous auctions

  • Bidders simultaneously submit a single bid for each item.

  • Each item is sold in a single-item auction.

    • First price item-bidding auction

    • Second price item-bidding auction - All-pay item-bidding auction

  • Efficient computation

  • Non-truthful mechanisms

• Example

• Not Truthful

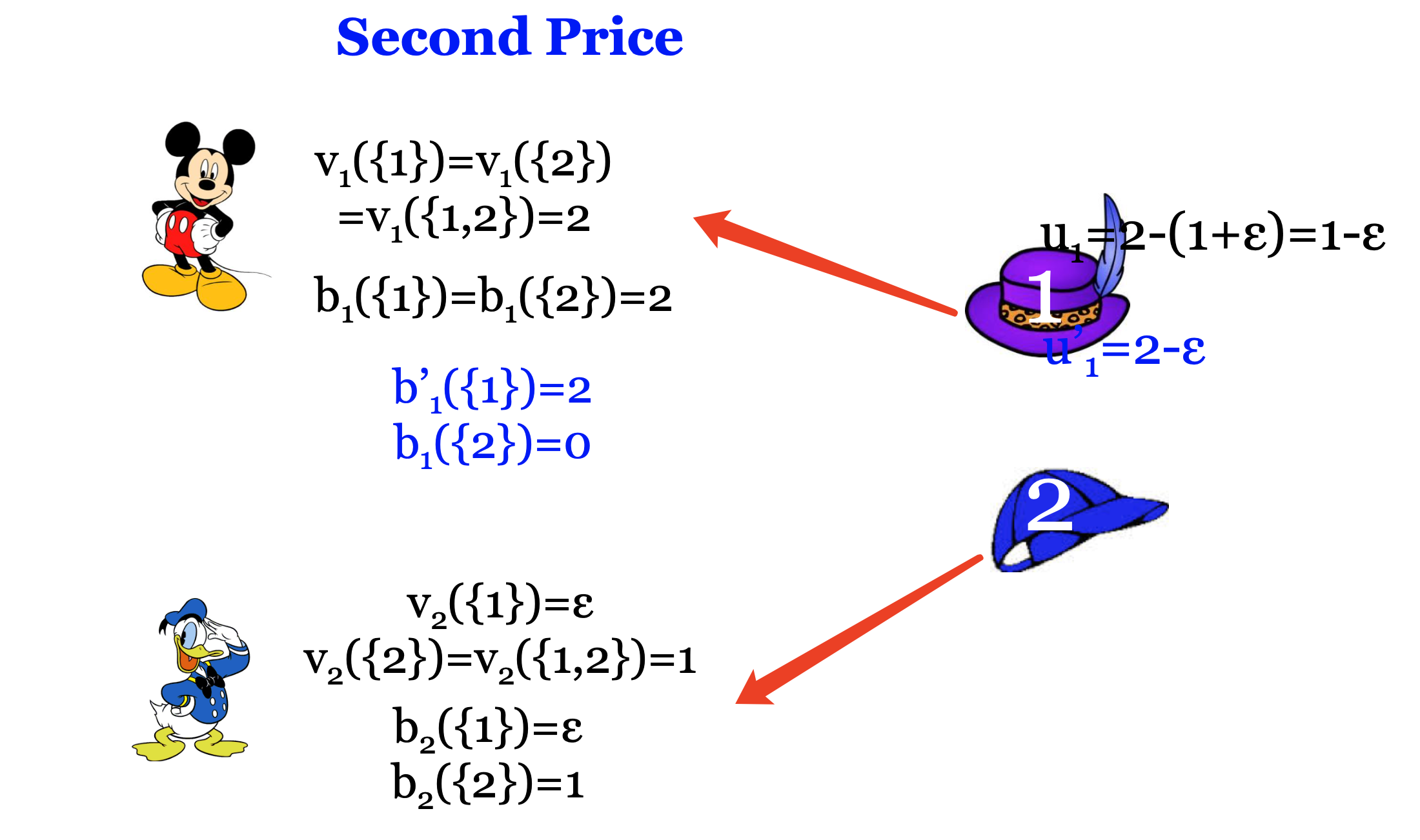
• PoA ≥ 2

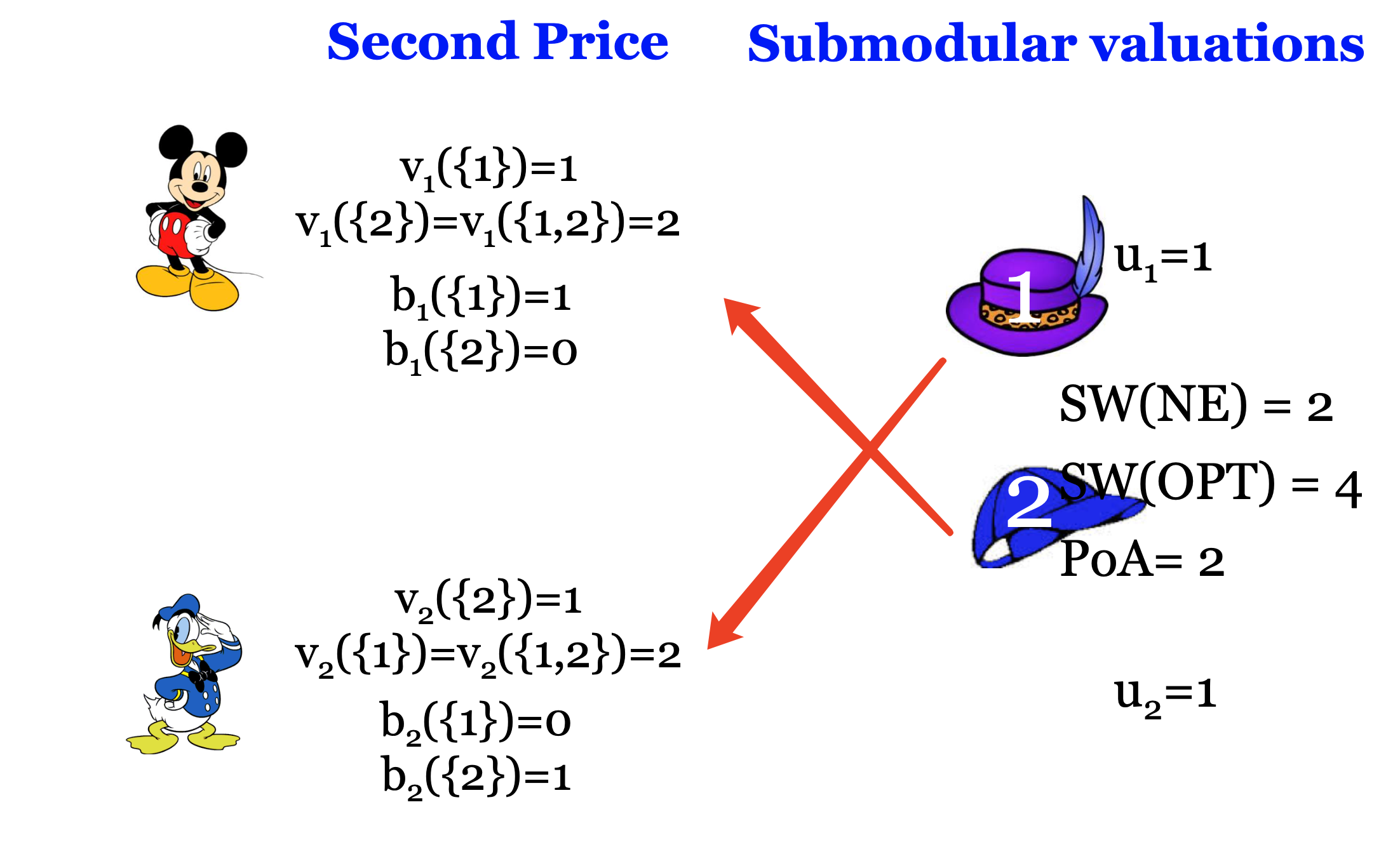
• PoA ≤ 4

The PoA of item-bidding (simultaneous) auctions is constant for using first, second or all-pay single-item auctions in subadditive valuations.

Food for thought

Suppose that we run a non-truthful mechanism that guarantees the following:

It maximizes the social welfare for (non-true) valuations vi(S) > v’i(S) > vi(S)/4 (where vi are the true valuation).

• What is the approximation to the optimal social welfare?

• Suppose that you have an incentive compatible mechanism with O(m1/2) approximation of the optimal social welfare. Is this a better mechanism? Why?

• Can you see the connection of the first mechanism to the PoA? How easy is it to find an equilibrium?