Flow Networks

• A flow network is a directed graph G=(V, E) with the following properties:

  • Each edge e in E has a nonnegative capacity ce.

  • There is a single source node s in V.

  • There is a single sink node t in V.

  • All other nodes in V - {s, t} are called internal nodes.

• Further assumptions:

  • The source s does not have any incoming edges.

  • The sink t does not have any outgoing edges.

  • There is at least one edge incident to each node.

  • All the capacities are integer numbers.

• Flow

• An (s-t) flow is a function f: E → R+, mapping each edge e to a nonnegative real number f(e).

• A (feasible) flow must satisfy the following two properties:

  • (Capacity) For each e in E, we have 0 ≤ f(e) ≤ ce

  • (Flow Conservation) For each node v in V - {s, t}, we have that

  

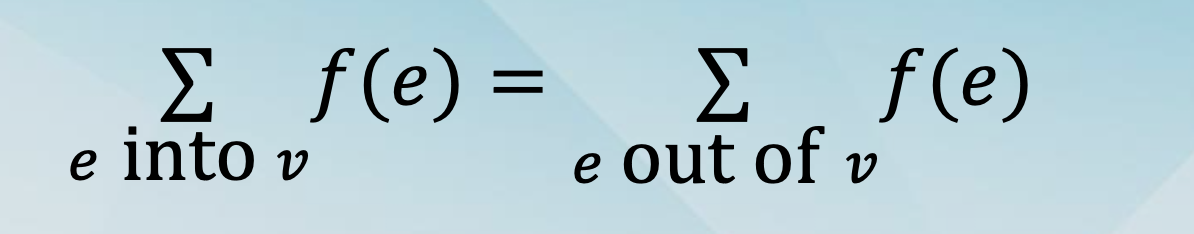
The Max Flow – Min Cut Theorem

• Minimum Cut

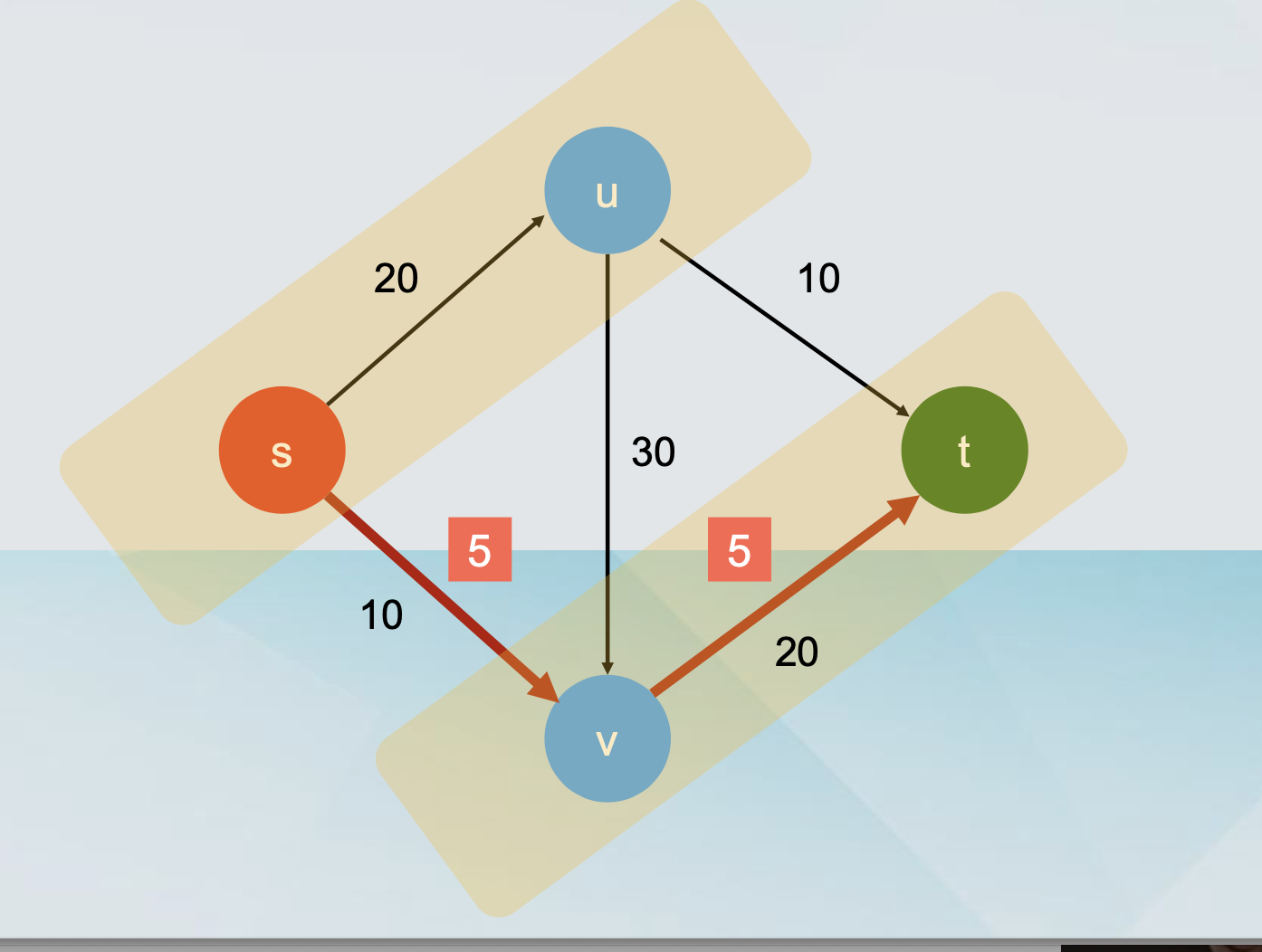
  • A cut C is a partition of the nodes of G into two sets S and T, such that s is in S and t is in T.

  • The capacity c(S,T) of a cut C is the sum of capacities of all edges “out of S”

    • these are edges (u, v) where u is in S and v is in T.

The Max-Flow Min-Cut Theorem

• Theorem: In every flow network, the value of the maximum flow is equal to the capacity of the minimum cut.

A series of facts

• Fact 1: Let f by any (s-t) flow and (S, T) be any (s-t) cut. Then v(f) = fout(S) - fin(S).

  

  • By definition, v(f) = fout(s).

  • By definition fin(s) = 0.

  • Hence, by definition v(f) = fout(s) - fin(s).

  • For every other node v≠s,t, we have fout(v) - fin(v) = 0

  

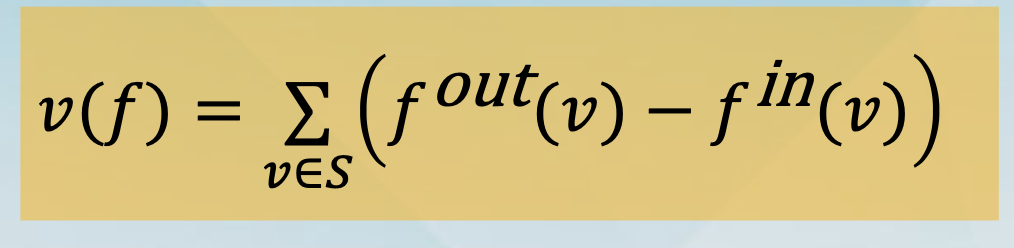
  • Let’s recount, using the edges and the flow f(e).

    • If an edge has both endpoints in S, it is counted once for “out” and once for “in”, so it contributes 0.

    • If an edge has its “tail” in S, it is only counted for “out” and contributes 1.

    • If an edge has its “head” in S, it is only counted for “in” and contributes -1.

    • Otherwise the edge does not appear in the sum.

  

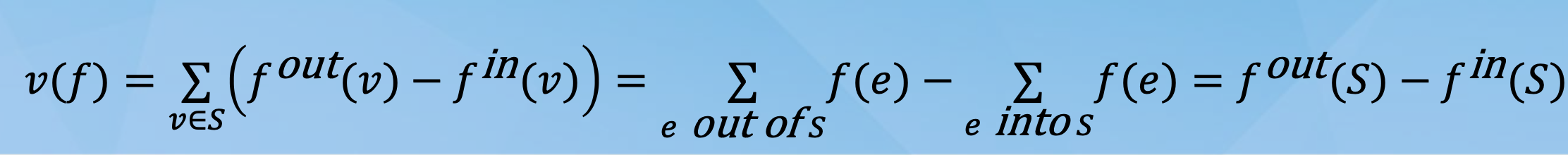
• Fact 2: Let f by any (s-t) flow and (S, T) be any (s-t) cut. Then v(f) = fin(T) - fout(T).

• Fact 3: Let f by any (s-t) flow and (S, T) be any (s-t) cut. Then v(f) ≤ c(S, T).

• Theorem: In every flow network, the value of the maximum flow is equal to the capacity of the minimum cut.

• Fact 4: Let f by any (s-t) flow in G such that the residual graph Gf has no augmenting paths. Then there is an (s-t) cut C(S*, T*) in G such that c(S*, T*) = v(f).

Constructing the cut

• In the residual graph Gf, identify the nodes that are reachable from the source s.

  • Put these in S*.

  • Put the rest in T*.

• Putting everything together

• Fact 4: Let f by any (s-t) flow in G such that the residual graph Gf has no augmenting paths. Then there is an (s-t) cut C(S*, T*) in G such that c(S*, T*) = v(f).

• Ford-Fulkerson stops when there are no augmenting paths(无增广路径) in the residual network.

• The value of the flow is equal to the capacity of some cut.

• This means that the value of the flow is maximum.

Integer-Valued Flows

• Fact 5: If all the capacities in the flow network are integers, there is maximum flow for which every flow value f(e) is an integer.

  • This follows from the properties of the Ford-Fulkerson algorithm.

  • It produces a maximum flow.

  • The capacities and flows are integers in every step of the execution.

Choosing Better Augmenting Paths