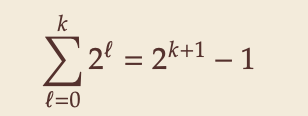Fundamental Data Structures

Data structures make heavy use of pointers and dynamically allocated memory.

Stacks & Queues

ATD: Abstract Data Types

ADT	data structures
list of supported operations	specify exactly
how data is represented
what should happen	algorithms for operations
not: how to do it	has concrete costs
(space and running time)
not: how to store data

Stack

• Operators
  • top(): Return the topmost item on the stack Does not modify the stack.
  • push(x): Add 𝑥 onto the top of the stack.
  • pop(): Remove the topmost item from the stack (and return it).

Queue

• Operators:
  • enqueue(x): Add 𝑥 at the end of the queue.
  • dequeue(): Remove item at the front of the queue and return it.

Resizable Arrays (可变大小的数组)

// Digression 题外话

• Array operations:
  • create(n)
  • get(i)
  • set(i, x)

Arrays have fixed size (supplied at creation).

Doubling trick

maintain capacity 𝐶 = 𝑆.length so that 14 𝐶 ≤ 𝑛 ≤ 𝐶

• How to maintain the last invariant?

  • before push: If 𝑛 = 𝐶, allocate new array of size 2𝑛, copy all elements.

  • after pop: If 𝑛 < 14 𝐶, allocate new array of size 2𝑛, copy all elements.

Amortized Analysis (摊销分析)

• Any individual operation push / pop can be expensive! Θ(𝑛) time to copy all elements to new array.

• But: An one expensive operation of cost 𝑇 means Ω(𝑇) next operations are cheap!

Formally: consider “credits/potential” Φ = min{𝑛 − 14 𝐶, 𝐶 − 𝑛} ∈ [0, 0.6𝑛]

amortized cost of an operation = actual cost (array accesses) − 4 · change in Φ

• cheap push/pop: actual cost 1 array access, consumes ≤ 1 credits ⇝ amortized cost ≤ 5
• copying push: actual cost 2𝑛 + 1 array accesses, creates 21 𝑛 + 1 credits ⇝ amortized cost ≤ 5
• copying pop: actual cost 2𝑛 + 1 array accesses, creates 12 𝑛 − 1 credits ⇝ amortized cost 5
• sequence of 𝑚 operations: total actual cost ≤ total amortized cost + final credits
  • here: ≤ 5𝑚 + 4·0.6𝑛 = Θ(𝑚+𝑛)

Priority Queues & Binary Heaps

Priority Queue ADT

elements in the bag have different priorities.

• Operators:

  • construct(𝐴): Construct from from elements in array 𝐴.
  • insert(𝑥,𝑝): Insert item 𝑥 with priority 𝑝 into PQ.
  • max(): Return item with largest priority. (Does not modify the PQ.)
  • delMax(): Remove the item with largest priority and return it.
  • changeKey(𝑥,𝑝′): Update 𝑥’s priority to 𝑝′. Sometimes restricted to increasing priority.

• PQ implementations

  • Elementary implementations
    • unordered list ⇝ Θ(1) insert, but Θ(𝑛) delMax
    • sorted list ⇝ Θ(1) delMax, but Θ(𝑛) insert

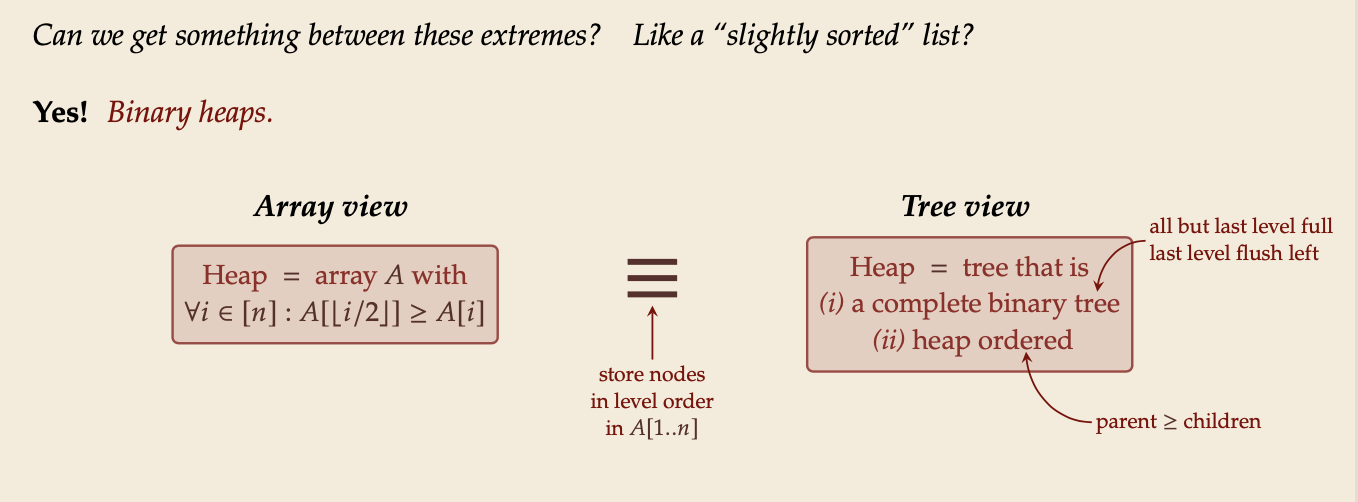
Why heap-shaped trees(堆形树)?

• Why complete binary tree shape?

  • only one possible tree shape
  • complete binary trees have minimal height among all binary trees
  • simple formulas for moving from a node to parent or children:
    • parent at ⌊𝑘/2⌋
    • left child at 2𝑘
    • right child at 2𝑘+1

• Why heap ordered?

  • Maximum must be at root!
  • But: Sorted only along paths of the tree; leaves lots of leeway for fast inserts

Operations on Binary Heaps

Insert

• Add new element at only possible place: bottom-most level, next free spot.

• Let element swim up(游上) to repair heap order.

Delete Max

• Remove max (must be in root).
• Move last element (bottom-most, rightmost) into root.
• Let root key sink in(沉入) heap to repair heap order.

Heap construction

• 𝑛 times insert ⇝ Θ(𝑛 log 𝑛)

• instead:

  • Start with singleton heaps (one element)
  • Repeatedly merge two heaps of height 𝑘 with new element into heap of height 𝑘 + 1

• Analysis

  • Height of binary heaps:
    • height of a tree: # edges on longest root-to-leaf path
    • depth/level of a node: # edges from root ⇝ root has depth 0 𝑘
    • How many nodes on first 𝑘 full levels?

Binary heap summary

Operation	Running Time
construct(𝐴[1…𝑛])	𝑂(𝑛)
max()	𝑂 (1)
insert(𝑥,𝑝)	𝑂(log 𝑛)
delMax()	𝑂(log 𝑛)
changeKey(𝑥,𝑝′)	𝑂(log 𝑛)
isEmpty()	𝑂 (1)
size()	𝑂 (1)